Interactions 1

Princeton University

Jason Geller, PH.D.(he/him)

2023-12-01

Packages

library(pacman)
p_load("tidyverse", "easystats", "broom", "kableExtra", "interactions", "emmeans", "moderndive", "ggeffects", "visreg")

Today

  • Testing interactions/moderation analysis

    • Categorical x Continuous
    • Continuous x Continuous

Interactions

lm(plant_growth ~ sun_exposure + water)

Interactions

  • Two variables can have joint effects, or interact with each other

What is a moderator?

  • A moderator variable Z (i.e., water) is a variable that alters the strength of the relationship between X and Y (sunshine -> growth)
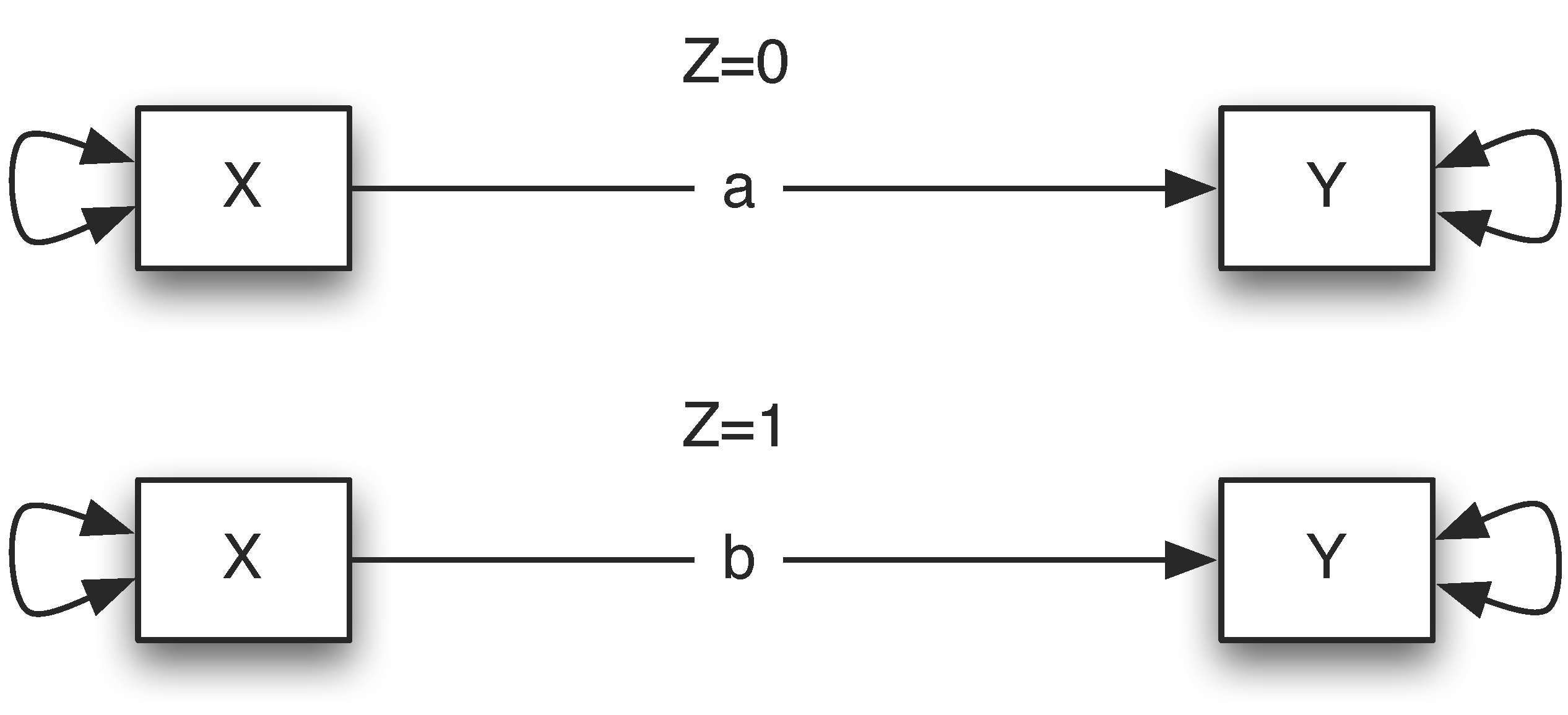
  • To test for moderation we can add the interaction between Z and X to our model

\[ \hat{Y}=b_{0}+b_{1}X (sunshine)+ b_2Z (water) + b_3X*Z\]

lm(plant_growth ~ sun_exposure * water)

What do interactions look Like?

Interaction shapes

  • Disordinal

    • Cross-over

Interaction shapes

  • Ordinal

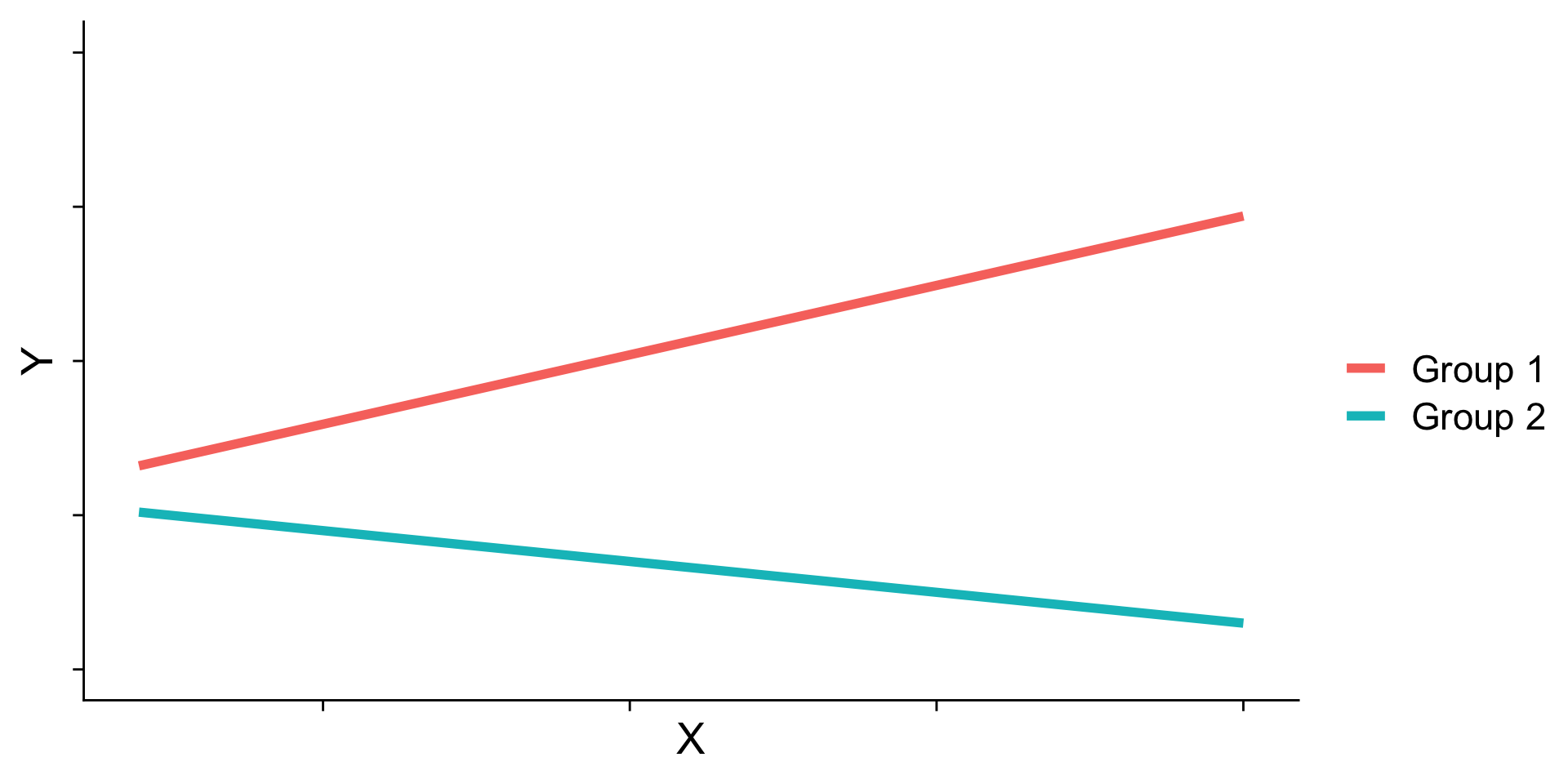
Interaction shapes

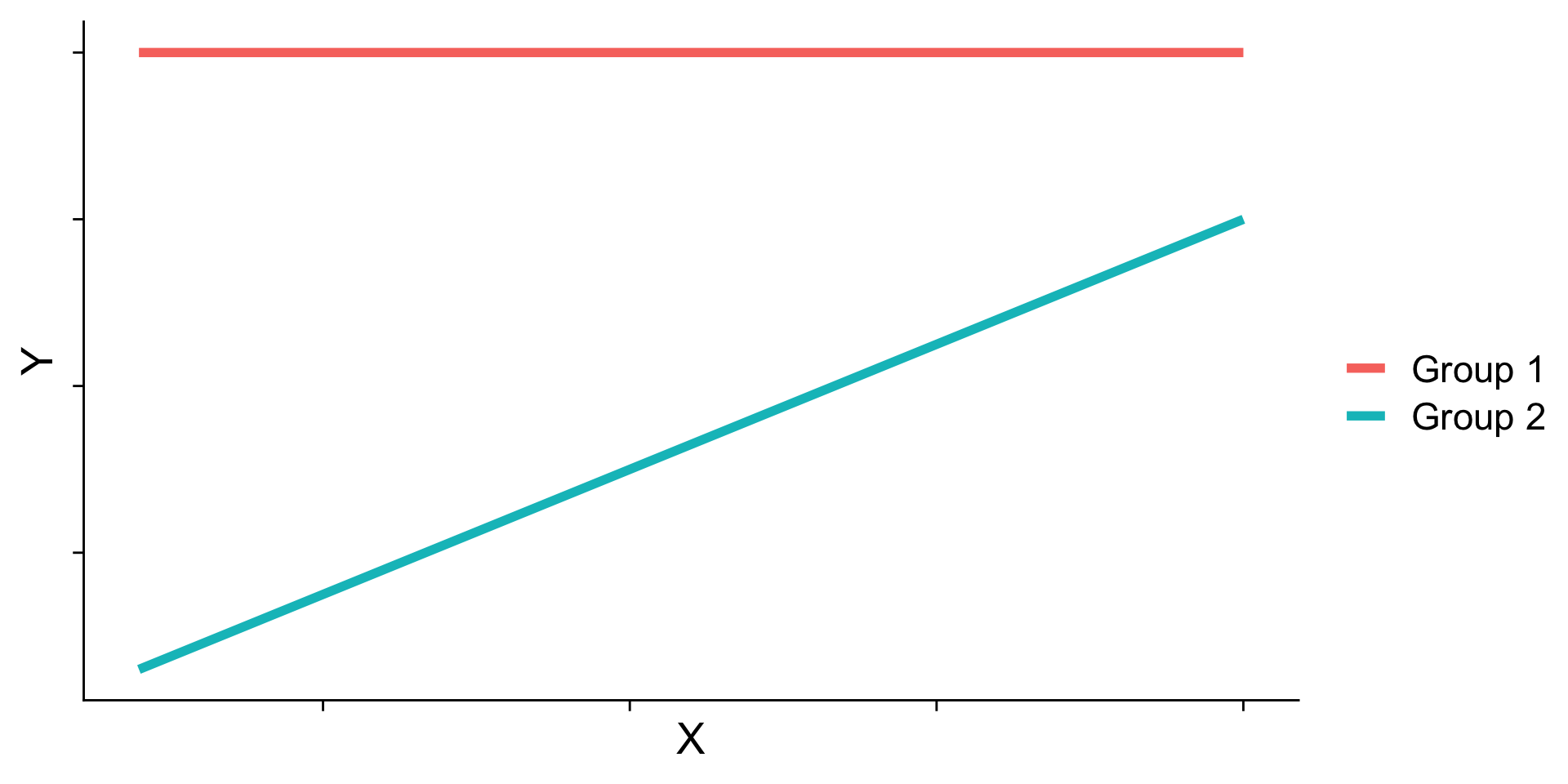
  • Ordinal

    • Knockout

Categorical x Continuous Interactions

Today’s dataset

  • Student evaluations for a sample of 463 courses taught by 94 professors from the University of Texas at Austin

  • Six students rated the professors’ physical appearance


    

  

  

  









Research question


    

  • Does Age and Sex (Males, Females) of the instructor influence instructor ratings?
    

      

    • DV: Evals
      • 

    • IV:

        

      • Age (continuous)
        • 

      • Gender (categorical)
        • 

      • Age*Gender interaction
        • 

      • 

    • 














Note






ANCOVA is a special case of a categorical x continuous regression model












Scatter plot



  
  

    

    

      

    

  

  

  









How to conduct moderation analysis?


    

  • Moderation analysis can be conducted by adding one or multiple interaction terms in a regression analysis
    • 

  • Z is a moderator for the relation between X and Y, we can fit a regression model
    • 



\[\begin{eqnarray*}
Y & = & b_{0}+b_{1}*X+b_{2}*Z+b_{3}*X*Z+e \\ & = & \begin{cases} b_{0}+b_{1}*X+e & \mbox{For females}(Z=0)\\ b_{0}+b_{2}+(b_{1}+b_{3})*X+e & \mbox{For males}(Z=1) \end{cases} \end{eqnarray*}\]


    

  • When Z=0 (females),the effect of X on Y is \(b_1+b_3∗0=b_1\)
    • 

  • When Z=1 (males), the effect of X on Y is \(b_1 + b_3*(1)\)
    • 







Steps for moderation analysis


A moderation analysis typically consists of the following steps:


    

  1. Compute the interaction term XZ=X*Z
    2. 

  2. Fit a multiple regression model with X, Z, and X*Z as predictors
    3. 

  3. Test whether the regression coefficient for XZ (interaction) is significant
    

    3.1 If so, interpret the moderation effect
    4. 

  4. Display the moderation effect graphically
    5. 







Steps for moderation analysis


    

  • Compute the interaction term XZ=X*Z
    • 




  
  

    

    

      

    

  

  

  









Steps for moderation analysis


    

  • Center continuous variables
    

      

    • Centering solves two problems:
      

        

      • Interpretation
        • 

      • Multicollinearity
        • 

      • 

    • 




  
  

    

    

      

    

  

  

  









Steps for moderation analysis


    

  • Fit a multiple regression model with X, Z, and X*Z as predictors
    • 

  • Test whether the regression coefficient for X*Z is significant
    • 




  
  

    

    

      

    

  

  

  









Interpretations


\[\hat{Y}= b_0 + b_1 X + b_2 Z + b_3 X*Z\]


where ( \(X\) ) is a continuous predictor and ( \(Z\) ) is a dummy coded categorical predictor.


    

  • \(b_0\): the intercept, or the predicted outcome when X = at mean and Z=0
    • 

  • \(b_1\): the slope of \(X\), for a one unit change in \(X\) the predicted change in \(Y\) at \(Z = 0\)
    • 

  • \(b_2\): The offset/difference in the intercept for a one unit change in \(Z\) the predicted change in Y at X = 0 (or at it’s mean)
    • 

  • \(b_3\): The interaction of \(X\) and \(Z\), the offset/difference in slope for \(Z\) for a one-unit increase in \(X\) (or vice versa)
    • 







Interpretations



  
  

    

    

      

    

  

  

  






  
  

    

    

      

    

  

  

  









Interpretations



  
  

    

    

      

    

  

  

  






  
  

    

    

      

    

  

  

  









Interpretations



  
  

    

    

      

    

  

  

  






  
  

    

    

      

    

  

  

  









Interpretations



  
  

    

    

      

    

  

  

  






  
  

    

    

      

    

  

  

  









Deviation coding



  
  

    

    

      

    

  

  

  






  
  

    

    

      

    

  

  

  









Moderation: simple slopes


    

  • If the interaction is significant, then you usually ignore the other individual effects (age and gender)
    • 

  • So what do I do if my interaction is significant?
    • 





    

  • A simple slopes/spotlight analysis
    • 









Steps for Moderation Analysis


    

  • Obtain simple slopes
    

      

    • The association between X and Y at different values of Z
      

        

      • Conditional analysis looking at the slope between different levels of the moderator
        

          

        • Test if slope \(\neq\) 0
          • 

        • 

      • 

    • 







Steps for moderation analysis



  
  

    

    

      

    

  

  

  









Steps for moderation analysis


    

  • A significant slope in one condition and not in another does not mean there is an interaction
    

      

    • Just testing if each slope is \(\neq\) 0
      • 

    • 

  • Must test the interaction!
    • 




  
  

    

    

      

    

  

  

  









Interactions


    

  • You should only be following up interactions if significant!
    • 








Visualize categorical by continuous interactions



  
  

    

    

      

    

  

  

  









Visualize Categorical by Continuous Interactions


    

  • Parallel slopes models still allow for different intercepts but force all lines to have the same slope
    • 




  
  

    

    

      

    

  

  

  









Parallel slopes


    

  • Model Comparisons
    

      

    • Test model without interaction to model with interaction
      • 

    • 




  
  

    

    

      

    

  

  

  









Parallel Slopes







  
  

    

    

      

    

  

  

  








  
  

    

    

      

    

  

  

  













Categorical x Continuous Write–up













Tip






All continuous predictors were mean-centered and deviation coding was used for categorical predictors. The results of the regression indicated that the model significantly predicted evaluation scores (R2 =0.05, F(3, 459) = 8.29, p <.001, adj. R2 = 0.05) accounting for 5% of the variance. Age was a significant negative predictor of scores, b = -0.01, SE = .003, 95% CI [-0.02, -0.01], t = -3.89, p < .001, with increases in age being associated with lower evals. Gender was also significant, b = -0.208, SE = .05, 95% CI [-0.312, -0.105], t = -3.95, p < .001, with women (M = 4.04) having lower evals than men (M =4.24). Importantly, there was a significant interaction between age and gender, b = -0.01, SE = .01, 95% CI [-0.02, -0.003], t = -2.45, p < .001). A simple slopes analysis indicated a significant slope for women, b = -0.02, SE = 0.004, 95% CI [-0.026, -0.009], t = -3.92, p < .001, but not men, b = 0.004, SE = 0.003, 95% CI [-0.01, 0.002], t = -1.23, p = 0.22. While age does not seem to affect evaluation scores for men, evaluation scores are poorer for older women.














Continuous x Continuous Interactions







Today’s other dataset



  
  

    

    

      

    

  

  

  





    

  • Do violent video games make people aggressive?
    

      

    • DV: Aggression
      • 

    • IV:
      

        

      • Callous unemotional traits (moderator)
        • 

      • Number of hours spent playing video games per week
        • 

      • Callous unemotional traits*Number of hours spent playing video games per week
        • 

      • 

    • 







Continuous x Continuous Interactions







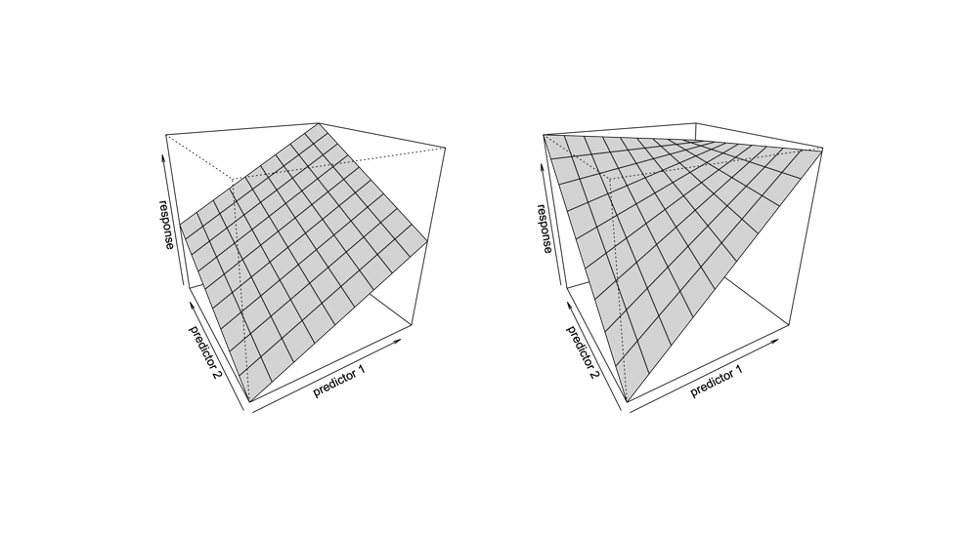
Continuous x Continuous Interactions


    

  • Centering
    

      

    • Can reduce multicollinearity
      • 

    • 




  
  

    

    

      

    

  

  

  









Interpretation Continuous x Continuous Interactions


\[\hat{Y}= b_0 + b_1 X + b_2 Z + b_3 X*Z\]


where ( \(X\) ) is a continuous predictor and ( \(Z\) ) is a continuous predictor.


    

  • \(b_0\): the intercept, or the predicted outcome when X = 0 and Z=0 (or at their means)
    • 

  • \(b_1\): the simple effect or slope of \(X\), for a one unit change in \(X\) the predicted change in \(Y\) at \(Z = 0\) (or at its mean)
    • 

  • \(b_2\): The simple effect or slope of \(Z\), for a one unit change in \(Z\) the predicted change in Y at X = 0 (or at its mean)
    • 

  • \(b_3\):The interaction of \(X\) and \(Z\), the change in the slope of \(X\) for a one-unit increase in \(Z\) (or vice versa)
    • 







Interpretation Continuous x Continuous Interactions



  
  

    

    

      

    

  

  

  






  
  

    

    

      

    

  

  

  









Interpretation Continuous x Continuous Interactions



  
  

    

    

      

    

  

  

  






  
  

    

    

      

    

  

  

  









Interpretation Continuous x Continuous Interactions



  
  

    

    

      

    

  

  

  






  
  

    

    

      

    

  

  

  









Interpretation Continuous x Continuous Interactions



  
  

    

    

      

    

  

  

  






  
  

    

    

      

    

  

  

  









Continuous X Continuous Interactions


    

  • If the Z (moderator variable) was categorical, you would be checking if separate groups (levels) have different slopes for the non-categorical variable
    • 

  • However, we cant do that with continuous x continuous interactions
    • 







Decomposing Continuous X Continuous Interactions: Spotlight Analysis


    

  • For continuous moderator variables, you “create” low, average, and high groups
    

      

    • Low groups are people who are one SD below the mean
      • 

    • Average groups are people are at the mean
      • 

    • High groups are people who are one SD above the mean
      • 

    • 







Probing Interactions: Spotlight Analysis


    

  • Low/below mean created by SUBTRACTING 1 SD
    • 

  • High/above mean created by ADDING 1 SD
    • 

  • The rule is that we have to bring them to the middle because we centered so that zero is the middle
    • 




  
  

    

    

      

    

  

  

  









Spotlight/simple slopes analysis



  
  

    

    

      

    

  

  

  







    

  • At average levels of callousness, the association between hours played and aggression is positive, b = .17
    • 




    

  • At high levels of callousness, the strength of hours of video games predicting aggression is the strongest, b = 0.43
    • 









Probing interactions


    

  • Use interact_plot from the interactions
    • 




  
  

    

    

      

    

  

  

  









Probing Interactions


    

  • ggpredict
    • 




  
  

    

    

      

    

  

  

  









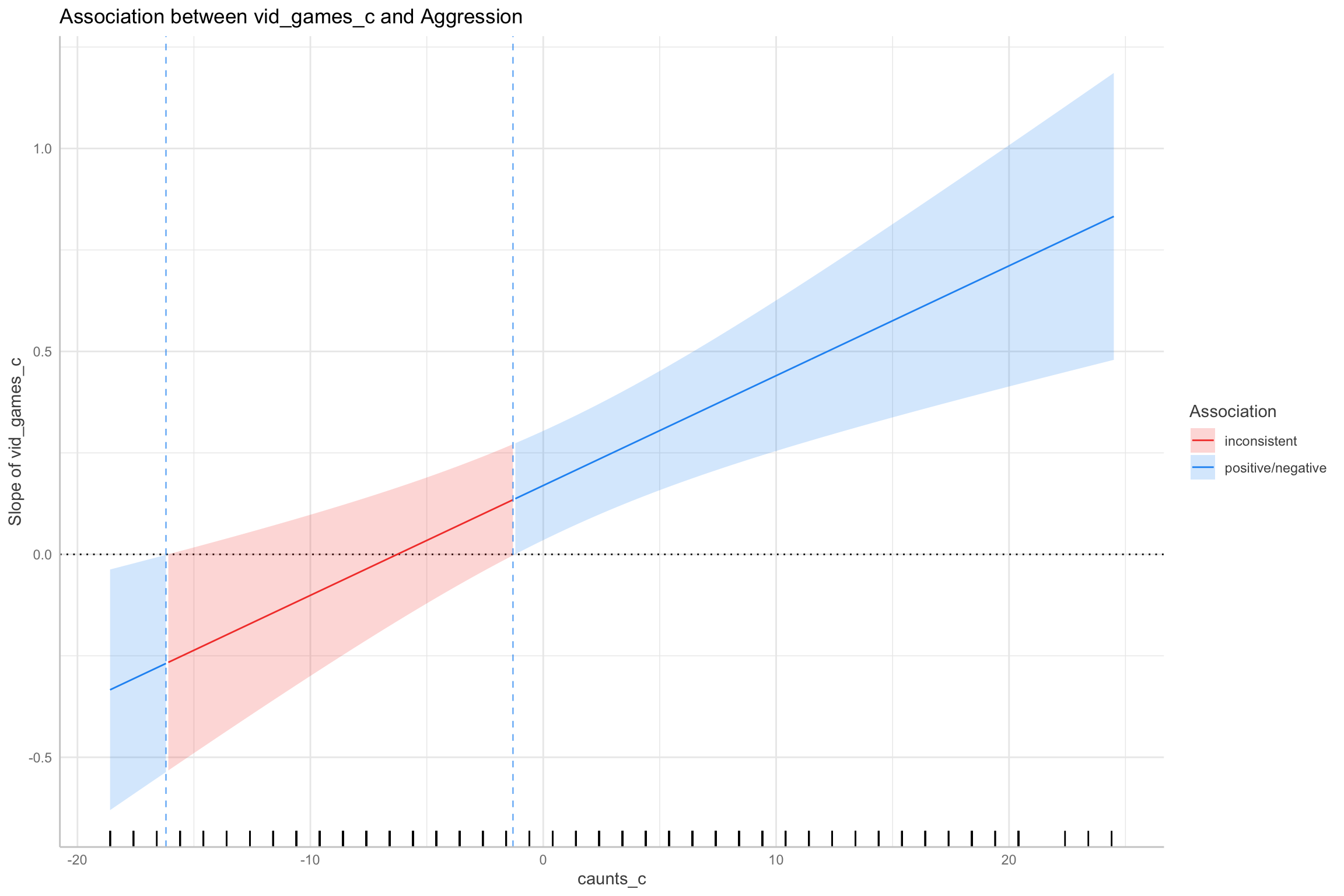
Probing interactions: Johnson-Neyman Plot


    

  • Floodlight analysis on the whole range of the moderator
    

      

    • Tests the slope at each observation of the moderator
      

        

      • Define a region of significance/non-significance across the slope
        • 

      • 

    • 







Probing interactions: Johnson-Neyman Plot








library(ggeffects)

pr <- ggpredict(d, c("vid_games_c", "caunts_c[all]"))
#correct for mult comparisons
hypothesis_test(pr, test=NULL, p_adjust = "holm") %>%
  kable()








vid_games_c
caunts_c
Slope
conf.low
conf.high
p.value






slope
-18.6
-0.3337320
-0.6302354
-0.0372286
0.5029953




slope
-17.6
-0.3066698
-0.5910010
-0.0223387
0.5879292




slope
-16.6
-0.2796076
-0.5519214
-0.0072938
0.7071445




slope
-15.6
-0.2525454
-0.5130128
0.0079219
0.8603115




slope
-14.6
-0.2254833
-0.4742998
0.0233333
1.0000000




slope
-13.6
-0.1984211
-0.4357799
0.0389378
1.0000000




slope
-12.6
-0.1713589
-0.3975433
0.0548256
1.0000000




slope
-11.6
-0.1442967
-0.3596104
0.0710171
1.0000000




slope
-10.6
-0.1172345
-0.3219646
0.0874956
1.0000000




slope
-9.6
-0.0901723
-0.2847782
0.1044336
1.0000000




slope
-8.6
-0.0631101
-0.2480262
0.1218060
1.0000000




slope
-7.6
-0.0360479
-0.2118081
0.1397122
1.0000000




slope
-6.6
-0.0089857
-0.1762247
0.1582532
1.0000000




slope
-5.6
0.0180764
-0.1413409
0.1774937
1.0000000




slope
-4.6
0.0451386
-0.1073294
0.1976066
1.0000000




slope
-3.6
0.0722008
-0.0742708
0.2186724
1.0000000




slope
-2.6
0.0992630
-0.0422840
0.2408100
1.0000000




slope
-1.6
0.1263252
-0.0114862
0.2641366
1.0000000




slope
-0.6
0.1533874
0.0180016
0.2887731
0.5029953




slope
0.4
0.1804496
0.0461251
0.3147740
0.1715909




slope
1.4
0.2075118
0.0728712
0.3421523
0.0545526




slope
2.4
0.2345739
0.0982114
0.3709365
0.0173187




slope
3.4
0.2616361
0.1222330
0.4010393
0.0058360




slope
4.4
0.2886983
0.1449861
0.4324105
0.0022012




slope
5.4
0.3157605
0.1666209
0.4649001
0.0009532




slope
6.4
0.3428227
0.1872151
0.4984303
0.0004810




slope
7.4
0.3698849
0.2068956
0.5328742
0.0002813




slope
8.4
0.3969471
0.2258419
0.5680523
0.0001865




slope
9.4
0.4240093
0.2440593
0.6039593
0.0001439




slope
10.4
0.4510715
0.2617204
0.6404225
0.0001252




slope
11.4
0.4781336
0.2788311
0.6774362
0.0001178




slope
12.4
0.5051958
0.2955640
0.7148277
0.0001178




slope
13.4
0.5322580
0.3119161
0.7525999
0.0001178




slope
14.4
0.5593202
0.3279754
0.7906650
0.0001178




slope
15.4
0.5863824
0.3436964
0.8290684
0.0001178




slope
16.4
0.6134446
0.3592578
0.8676313
0.0001178




slope
17.4
0.6405068
0.3745389
0.9064746
0.0001178




slope
18.4
0.6675690
0.3896822
0.9454557
0.0001178




slope
19.4
0.6946311
0.4046855
0.9845768
0.0001178




slope
20.4
0.7216933
0.4195149
1.0238718
0.0001220




slope
22.4
0.7758177
0.4487827
1.1028527
0.0001329




slope
23.4
0.8028799
0.4633260
1.1424338
0.0001382




slope
24.4
0.8299421
0.4777436
1.1821405
0.0001439
















plot(johnson_neyman(pr, p_adjust = "holm"), show_rug=TRUE)




The association between `vid_games_c` and `Aggression` is negative for
  values of `caunts_c` lower than -16.20 and positive for values higher
  than -1.30. Inside the interval of [-16.20, -1.30], there were no clear
  associations. 




























Continuous x continuous write-up













Tip

















Important






All continuous predictors were mean-centered. The results of the regression indicated that the model significantly predicted violent behavior scores (R2 = 0.38,F(3, 438) = 88.46, p < .001, adj.R2 = 0.37) accounting for 37% of the variance. Hours was a significant positive predictor of violence, b = 0.17, SE = .07, 95% CI [0.04, 0.3], t = 2.48, p < .014, with increases in hours played being associated with higher levels of violence. Callous traits was also a positive predictor of violence, b = 0.76, SE = .05, 95% CI [0.51, 0.65], t = 15.37, p < .001, with increases in callous traits being associated with higher levels of violence. Importantly, there was a significant interaction between hours played and callous traits, b = 0.03, SE = .01, 95% CI [0.01, 0.04], t = 3.88, p < .001). Following up with a simple slopes/spotlight analysis showed the effect was significant at average levels of callous traits, b = -0.42, SE= 0.09, t = 4.64, p < .0001 and high levels of callous traits, b = -0.42, SE= 0.09, t = 4.64, p < .0001, but not at low levels of callous traits, b = -0.09, SE= 0.10, t = -0.911, p = 0.36 Thus, hours playing video games and violent scores is moderated by callous traits. Specifically, the relationship between hours playing video games and violence scores is strongest for those with high callous traits.


















Continuous x continuous write-up


    

  • JN Technique
    • 














Tip






Since the moderator (callous traits) was continuous, we looked for the turning points for where exactly, in the value of the moderator, the effect of the independent variable (Hours) turns from non-significance to significance (for a pre-specified significance level of 0.05). This is done using the Johnson–Neyman technique. The Johnson–Neyman technique showed that at the association between hours played and aggression is positive for values higher than -1.30. Inside the interval of [-16.20, -1.30], there were no clear associations. There is a detrimental effect between hours played and aggression at high levels of callous traits.












Moderation: MeMoBootR


    

  • We can use the MeMoBootR to complete the entire processing, including data screening for us!
    • 

  • You would enter the raw variables, as the centering is completed for you
    • 





#devtools::install_github("doomlab/MeMoBootR")
library(MeMoBootR)

moderation_vio=read.csv("https://raw.githubusercontent.com/jgeller112/psy503-psych_stats/master/moderation.csv")

mod_model <- moderation1(y = "Aggression",
                         x = "Vid_Games",
                         m = "CaUnTs",
                         df = moderation_vio)








Moderation: MeMoBootR




#|eval: false
#|
#data screenin
#mod_model$datascreening$fulldata
#models
#summary(mod_model$model1)
#mod_model$interpretation
#graphs
#mod_model$graphslopes








Power




WebPower::wp.regression(n=NULL, p1=3, p2=0, f2=.2, alpha=.05, power=.9)




Power for multiple regression

          n p1 p2  f2 alpha power
    74.8939  3  0 0.2  0.05   0.9

URL: http://psychstat.org/regression










Power





#install.packages("InteractionPoweR")
library(InteractionPoweR)




    

  • All we need is:
    

      

    • Correlations
      

        

      • X-Y
        • 

      • Z-Y
        • 

      • XZ-Y
        • 

      • X-Z
        • 

      • 

    • 







Next time


    

  • Categorical x categorical interactions
    • 







Cited




PSY 503: Foundations of Statistics in Psychology







Baranger, David A. A., Megan C. Finsaas, Brandon L. Goldstein, Colin E. Vize, Donald R. Lynam, and Thomas M. Olino. 2023. “Tutorial: Power Analyses for Interaction Effects in Cross-Sectional Regressions.” Advances in Methods and Practices in Psychological Science 6 (3). https://doi.org/10.1177/25152459231187531.