Monsters, Models, and Normal Distributions

Princeton University

Jason Geller, PH.D.(he/him)

2023-10-02

Announcements

Gavin Simpson will be here tomorrow giving a talk on non-linearity in modeling and generalized additive models (should be introductory)
I would like you to send me a description of the paper and data you want to re-analyze by end of the month
Readings
- Don’t feel like you have to complete all the code and questions from textbook
  - At the bare minimum, I just want you to read the chapters
We have class on Wednesday, but no lab
No webr in slides yet (but notes on website do)

Outline

Thinking about models
The normal distribution
Z-scores

Packages

library(grateful)
pkgs <- cite_packages(output = "table", out.dir = ".")

pkgs

      Package Version                                       Citation
1        base   4.2.2                                          @base
2     cowplot   1.1.1                                       @cowplot
3  datawizard 0.8.0.4                                    @datawizard
4   easystats 0.6.0.8                                     @easystats
5      ggdist   3.2.0                                        @ggdist
6       knitr    1.41             @knitr2014; @knitr2015; @knitr2022
7      pacman   0.5.1                                        @pacman
8   rmarkdown    2.14 @rmarkdown2018; @rmarkdown2020; @rmarkdown2022
9   supernova   2.5.6                                     @supernova
10  tidyverse   1.3.2                                     @tidyverse
11 tigerstats   0.3.2                                    @tigerstats

What is a statistical model?

Statistical modeling = “making models of distributions”

What is a model?

Models are simplifications of things in the real world

What is a model?

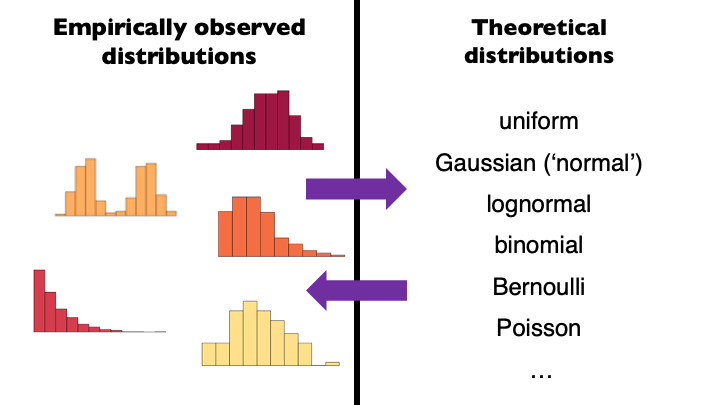
Distributions

Basic Structure of a Statistical Model

\[data = model + error\]

Data
Model
- Use our model to predict the value of the data for any given observation:
  
  \[\widehat{data_i} = model_i\]
Error (predicted - observed)

\[error_i = data_i - \widehat{data_i}\]

Models as Monsters

The Golem of Prague
- The golem was a powerful clay robot
- Brought to life by writing emet (“truth”) on its forehead
- Obeyed commands literally
- Powerful, but no wisdom
- In some versions, Rabbi Judah Loew ben Bezalel built a golem to protect
  - But he lost control, causing innocent deaths

Statistical golems

Statistical (and scientific) models are our golems
- We build them from basic parts
- They are powerful—we can use them to understand the world and make predictions
- They are animated by “truth” (data), but they themselves are neither true nor false
- The model describes the golem, not the world
  - The model doesn’t describe the world or tell us what scientific conclusion to draw—that’s on us
- We need to be careful about how we build, interpret, and apply models!

Choosing a Statistical Model

Cookbook approach
- Do Smarties make us smarter?
  - Take 200 7-year-olds
    - Randomly assign to 2 groups
      - Control: Normal breakfast
      - Treatment: Normal breakfast + 1 packet of Smarties
      - Outcome: Age-appropriate general reasoning test

Choosing a Statistical Model

Cookbook approach
- Every one of these tests is the same model
- The general linear model (GLM)

The cookbook approach makes it hard to think clearly about relationship between our question and the statistics

The General Linear Model

General mathematical framework
- Regression all the way down
- Highly flexible
  - Can fit qualitative (categorical) and quantitative predictors
- Easy to interpret
- Helps understand interrelatedness to other models
- Easy to build to more complex models

The General Linear Model

Modeling comparison approach
Think in terms of models and not tests
Model is determined by question, not data
What do alternative models say about the world?
Let’s build a model for this experiment

A simple model

General reasoning scores

# The Data
control_group= c(92, 97, 123, 101, 102, 126, 107, 81, 90, 93, 118, 105, 106, 102, 92, 127, 107, 71, 111, 93, 84, 97, 85, 89, 91, 75, 113, 102, 83, 119, 106, 96, 113, 113, 112, 110, 108, 99, 95, 94, 90, 97, 81, 133, 118, 83, 94, 93, 112, 99, 104, 100, 99, 121, 97, 123, 77, 109, 102, 103, 106, 92, 95, 85, 84, 105, 107, 101, 114, 131, 93, 65, 115, 89, 90, 115, 96, 82, 103, 98, 100, 106, 94, 110, 97, 105, 116, 107, 95, 117, 115, 108, 104, 91, 120, 91, 133, 123, 96, 85)


treat_group= c(99, 114, 106, 105, 96, 109, 98, 85, 104, 124, 101, 119, 86, 109, 118, 115, 112, 100, 97, 95, 112, 96, 103, 106, 138, 100, 114, 111, 96, 109, 132, 117, 111, 104, 79, 127, 88, 121, 139, 88, 121, 106, 86, 87, 86, 102, 88, 120, 142, 91, 122, 122, 115, 95, 108, 106, 118, 104, 125, 104, 126, 94, 91, 159, 104, 114, 120, 103, 118, 116, 107, 111, 109, 142, 99, 94, 111, 115, 117, 103, 94, 129, 105, 97, 106, 107, 127, 111, 121, 103, 113, 105, 111, 97, 90, 140, 119, 91, 101, 92)

df <- tibble(treatment=treat_group, control=control_group)

df_candy <- df %>%
  pivot_longer(treatment:control, names_to = "cond", values_to = "values")

Building a Model - Notation

Small Roman letters
- Individual observed data points
  - \(y_1\), \(y_2\), \(y_3\), \(y_4\), …, \(y_n\)
    - The scores for person 1, person 2, person 3, etc.
  - \(y_i\)
    - The score for the “ith” person

Big Roman letters
- A “random variable”
- The model for data we could observe, but haven’t yet
\(Y_1\)
- The model for person 1
- The yet-to-be-observed score of person 1

Building a Model - Notation

Greek letters
- Population parameters
- Unobservable parameters
μ
- mu
  - “mew” - Used to describe means
σ
- Sigma
- Used to describe a standard deviation

Building a Model - Notation

Roman letters
- Sample specific statistics
  - \(\bar{X}\) - sample mean
  - s - standard deviation from the sample
- Data estimates
  - \(b_0\)

A simple model

Null or empty model

\[ Y_i = \beta_0 + \epsilon \]

\[ Y_i= b_0 + e \]

Makes the same prediction for each observation

A Simple Model: Data

Scores
101
114
131
9

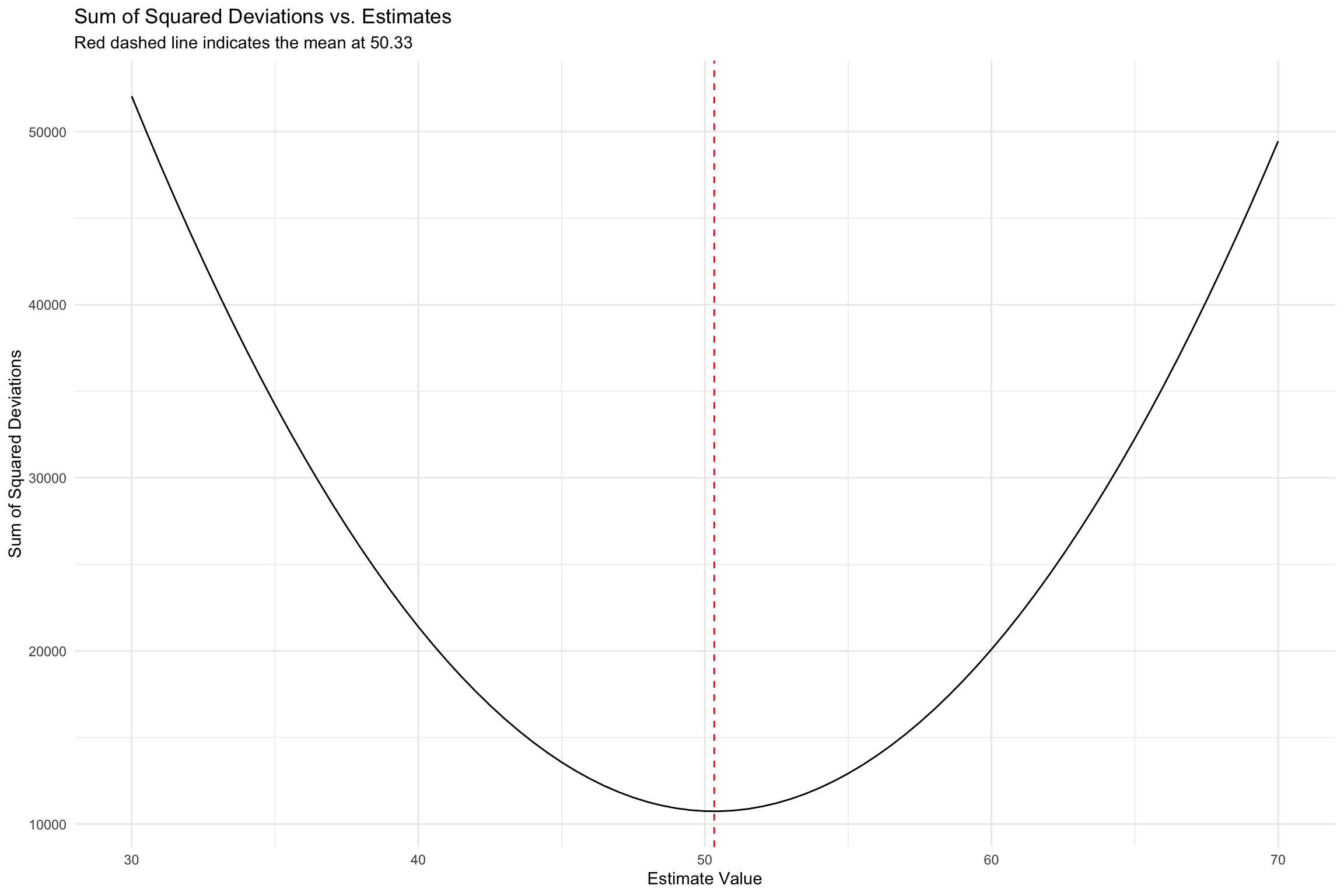
Figuring out \(b_0\)

Goal of any model is to find an estimator that minimizes the error
- How we define error will determine the best estimator

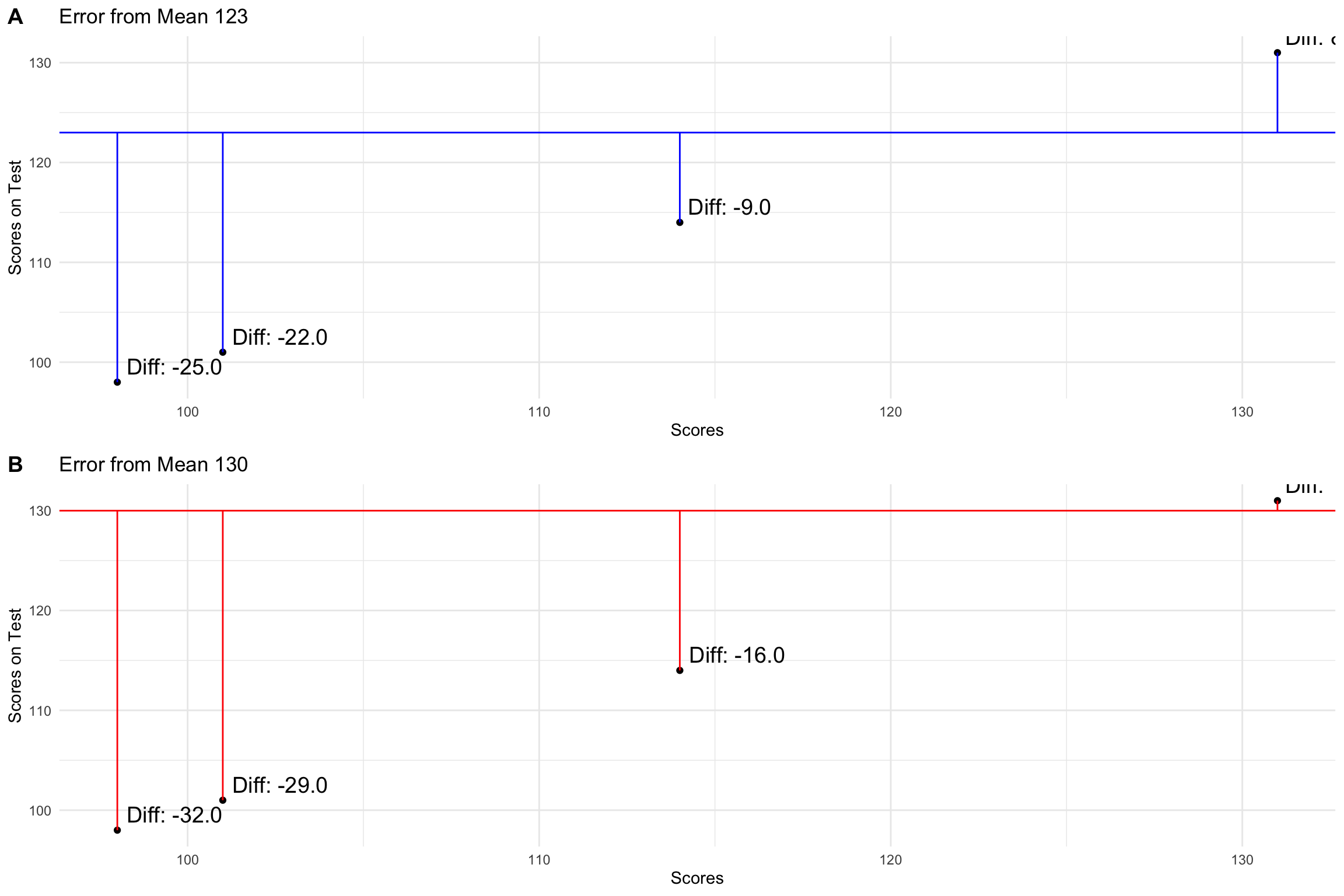
Types of Errors

Sum of errors (residuals)

The sum of the differences between observed values and predicted values. In an ideal case with no bias, this would be zero.

\[SE = \sum_{i=1}^{n} (y_i - \hat{y}_i)\]

Sum of absolute errors

Measures the total absolute difference between observed and predicted values. It gives a sense of the average magnitude of errors without considering direction

\[SAE = \sum_{i=1}^{n} |y_i - \hat{y}_i|\]

Median is best estimate for \(b_0\)

Sum of squares (SS)

This measures the total squared difference between observed and predicted values
Most commonly used in regression analysis (what we will be using)

\[SS = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2\]

The mean

Mean is the best estimator of \(b_0\)

\[\frac{1}{n} \sum_{i=i}^{n} x_{i}\]

Mean has really nice proprieties: \[SE = \sum_{i=1}^{n} (y_i - \hat{y}_i)\]

SSR minimized at mean

SSR minimized at mean

Describing error

We should have some overall description of the accuracy of model’s predictions
- SSR
  - Standard deviation
    
    \[ s^2 = \text{MSE} = \frac{1}{n-p} \sum_{i=1}^{n} (Y_i - \hat{Y}_i)^2 \]

\[ \text{SD} = \sqrt{\text{MSE}} \]

Statistical Modeling: A Concrete Example

Let’s look at general reasoning scores

  df_candy  %>%
  ggplot(aes(x=values)) +
  geom_dotsinterval()

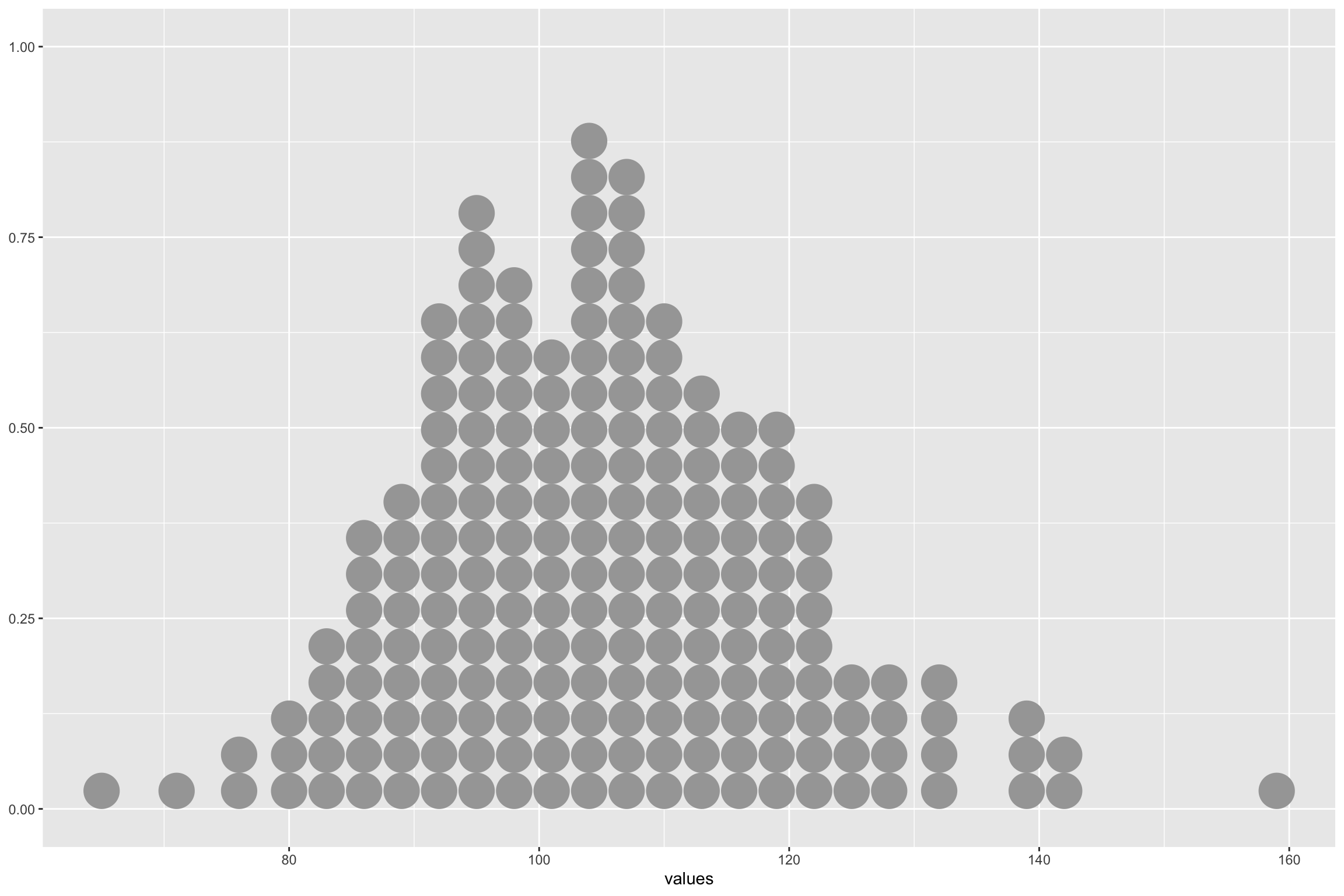
Building a Model - Concrete example

\[ Y_i = b_0 + e \]

What is the overall mean of the dataset?

# calcuate the mean

Building a Model - Concrete example

lm function in R can fit an empty model

null_model <- lm(values~NULL, data=df_candy)

null_model


Call:
lm(formula = values ~ NULL, data = df_candy)

Coefficients:
(Intercept)  
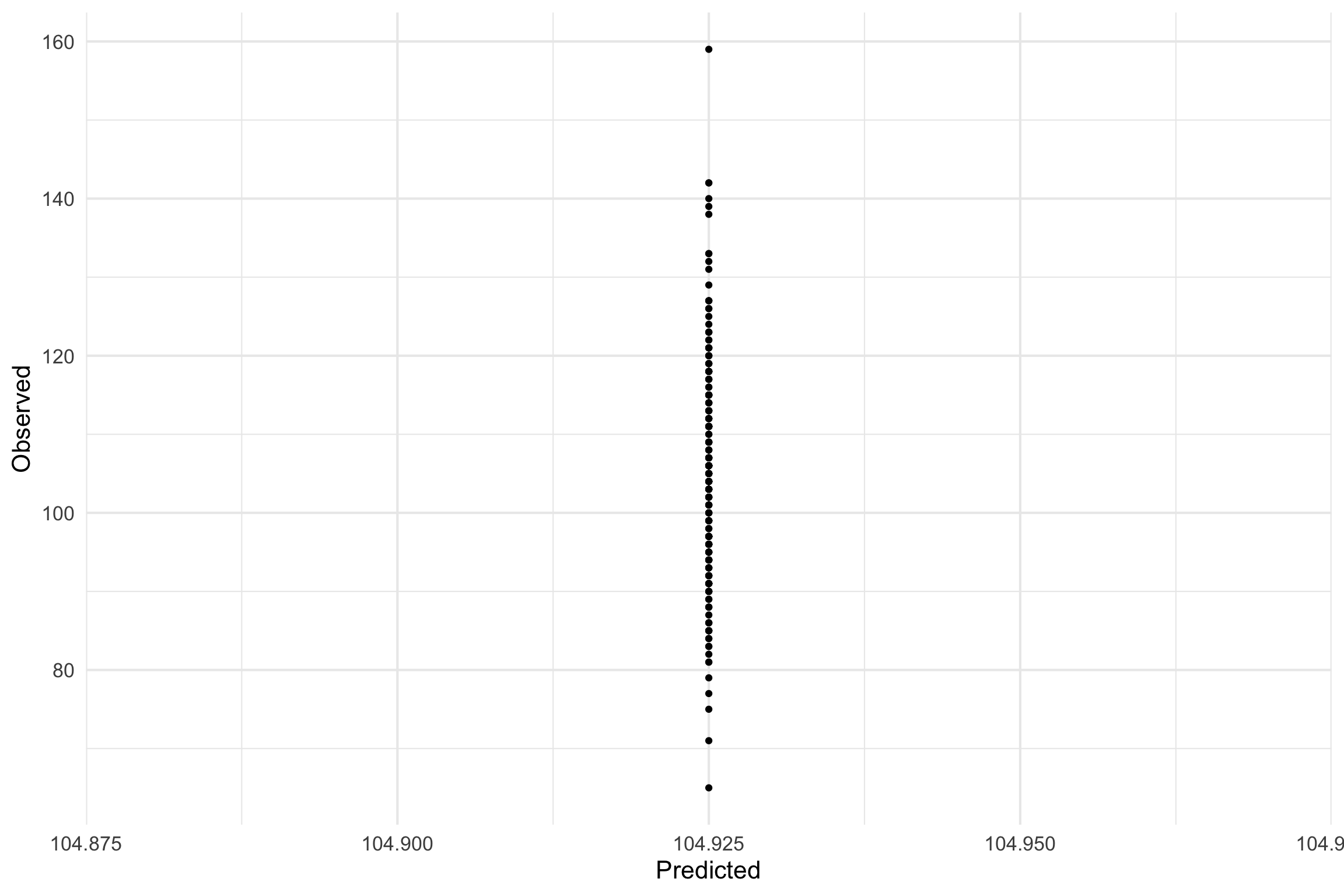
      104.9

\(b_0\) = Intercept = Estimate = Mean

Building a Model - Concrete example

broom is a helper package that provides us with lots of useful functions to get things like residuals, predicted values, etc)

library(broom)

null_model <- lm(values~NULL, data=df_candy)

null_model %>%
  broom::augment()

# A tibble: 200 × 7
   values .fitted   .resid    .hat .sigma     .cooksd .std.resid
    <dbl>   <dbl>    <dbl>   <dbl>  <dbl>       <dbl>      <dbl>
 1     99    105.  -5.92   0.00500   14.6 0.000839      -0.409  
 2     92    105. -12.9    0.005     14.5 0.00399       -0.891  
 3    114    105.   9.08   0.005     14.6 0.00197        0.626  
 4     97    105.  -7.92   0.005     14.6 0.00150       -0.547  
 5    106    105.   1.08   0.005     14.6 0.0000276      0.0741 
 6    123    105.  18.1    0.005     14.5 0.00781        1.25   
 7    105    105.   0.0750 0.005     14.6 0.000000134    0.00517
 8    101    105.  -3.92   0.005     14.6 0.000368      -0.271  
 9     96    105.  -8.92   0.005     14.6 0.00190       -0.616  
10    102    105.  -2.92   0.005     14.6 0.000205      -0.202  
# ℹ 190 more rows

Building a model - Concrete example

Can get SS a few different ways

null_model %>% 
  broom::augment()%>%
  # take the sum of the resid column squared
  summarise(SS=(sum(.resid^2)))

# A tibble: 1 × 1
      SS
   <dbl>
1 42044.

Building a model - Concrete Example

Building a model - Concrete example

aov(lm(null_model))

Call:
   aov(formula = lm(null_model))

Terms:
                Residuals
Sum of Squares   42043.87
Deg. of Freedom       199

Residual standard error: 14.53533

library(supernova)

supernova(null_model)

 Analysis of Variance Table (Type III SS)
 Model: values ~ NULL

                                SS  df      MS   F PRE   p
 ----- --------------- | --------- --- ------- --- --- ---
 Model (error reduced) |       --- ---     --- --- --- ---
 Error (from model)    |       --- ---     --- --- --- ---
 ----- --------------- | --------- --- ------- --- --- ---
 Total (empty model)   | 42043.875 199 211.276

Building a model - concrete example

Mean squared error (MSE)

null_model %>% 
  broom::augment()%>%
  summarise(SS=(sum(.resid^2)), MSE_v=SS/(199), MSE_sd= sqrt(MSE_v)) %>% knitr::kable()

SS	MSE_v	MSE_sd
42043.88	211.2758	14.53533

supernova(null_model)

 Analysis of Variance Table (Type III SS)
 Model: values ~ NULL

                                SS  df      MS   F PRE   p
 ----- --------------- | --------- --- ------- --- --- ---
 Model (error reduced) |       --- ---     --- --- --- ---
 Error (from model)    |       --- ---     --- --- --- ---
 ----- --------------- | --------- --- ------- --- --- ---
 Total (empty model)   | 42043.875 199 211.276

Building a model - Concrete example

Predictions from the model

null_model %>%
  augment() %>%

ggplot(aes(x = .fitted, y=values)) + 
  geom_point() +
  theme_minimal(base_size = 16) + 
  labs(y = "Observed", x = "Predicted")

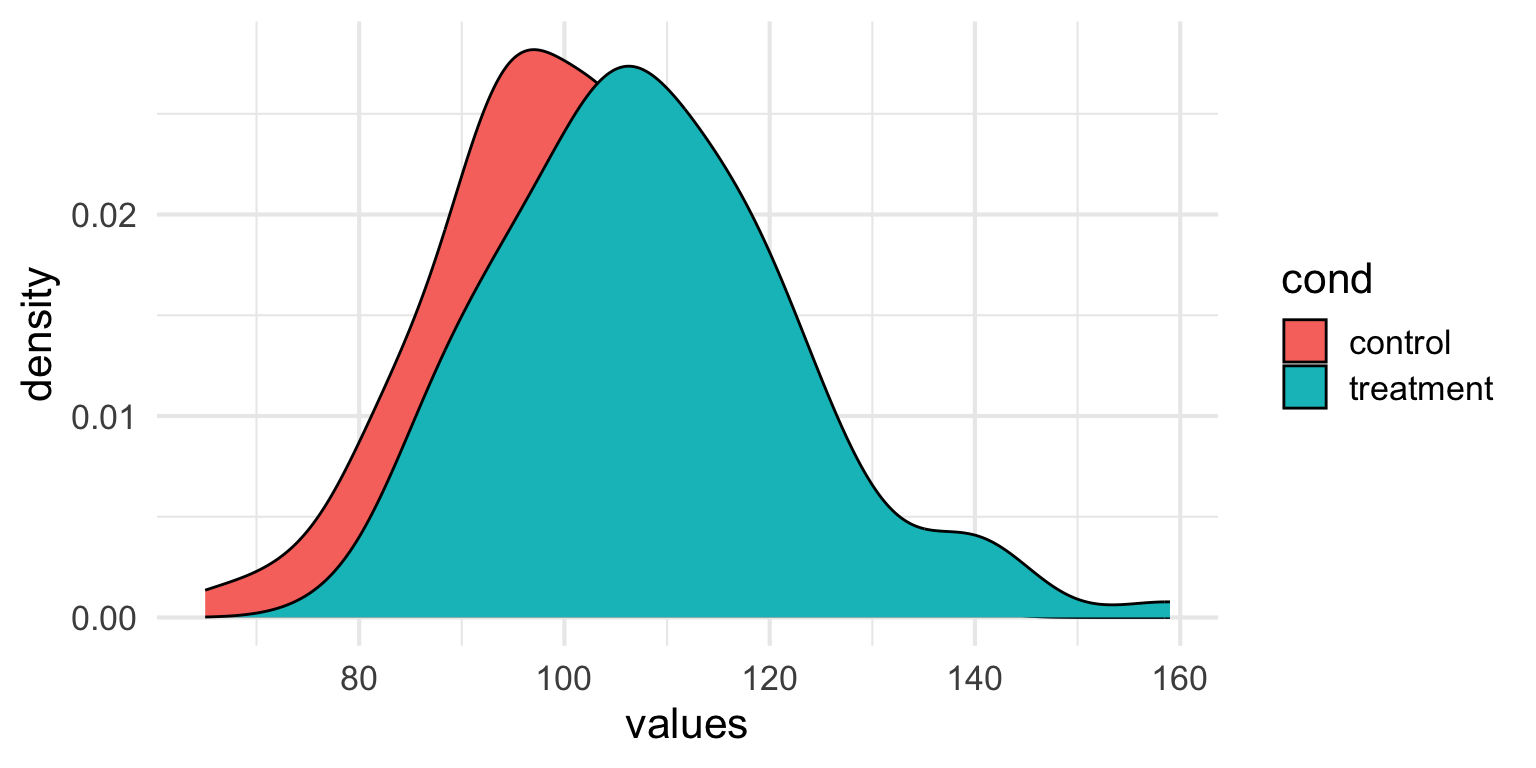
A More Complex Model

Do you think the empty model is a good model?

What Makes a Model “Good”

We want it to describe our data well
We want it to generalize to new datasets
- We want error to be as small as possible

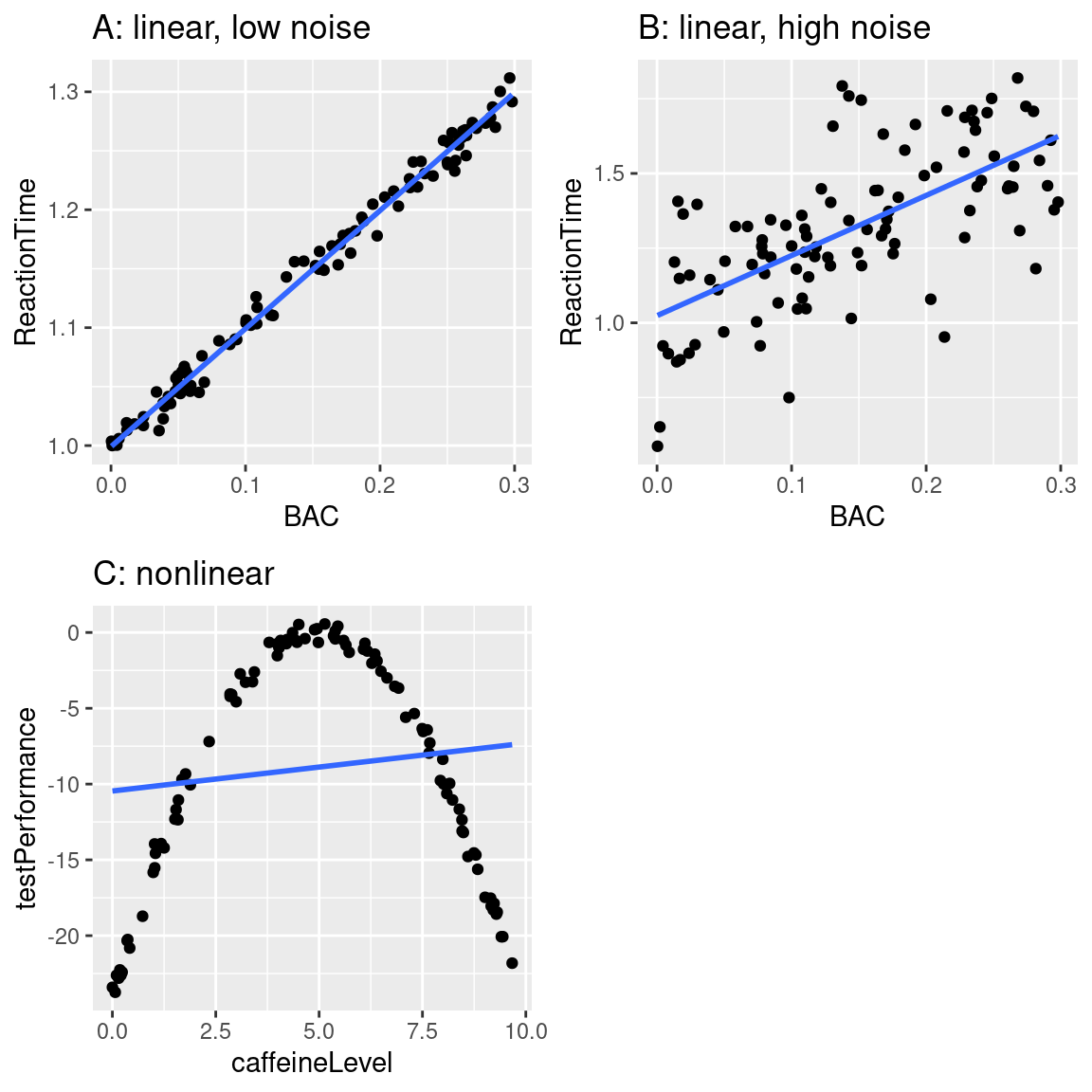
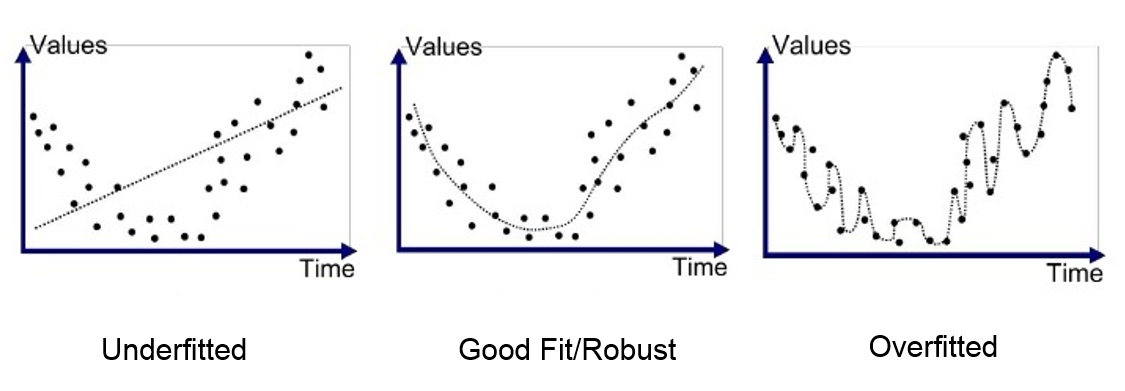
Can a Model Be Too Good?

Yes!
- Overfitting
  - A model with little to no error will not generalize to new datasets

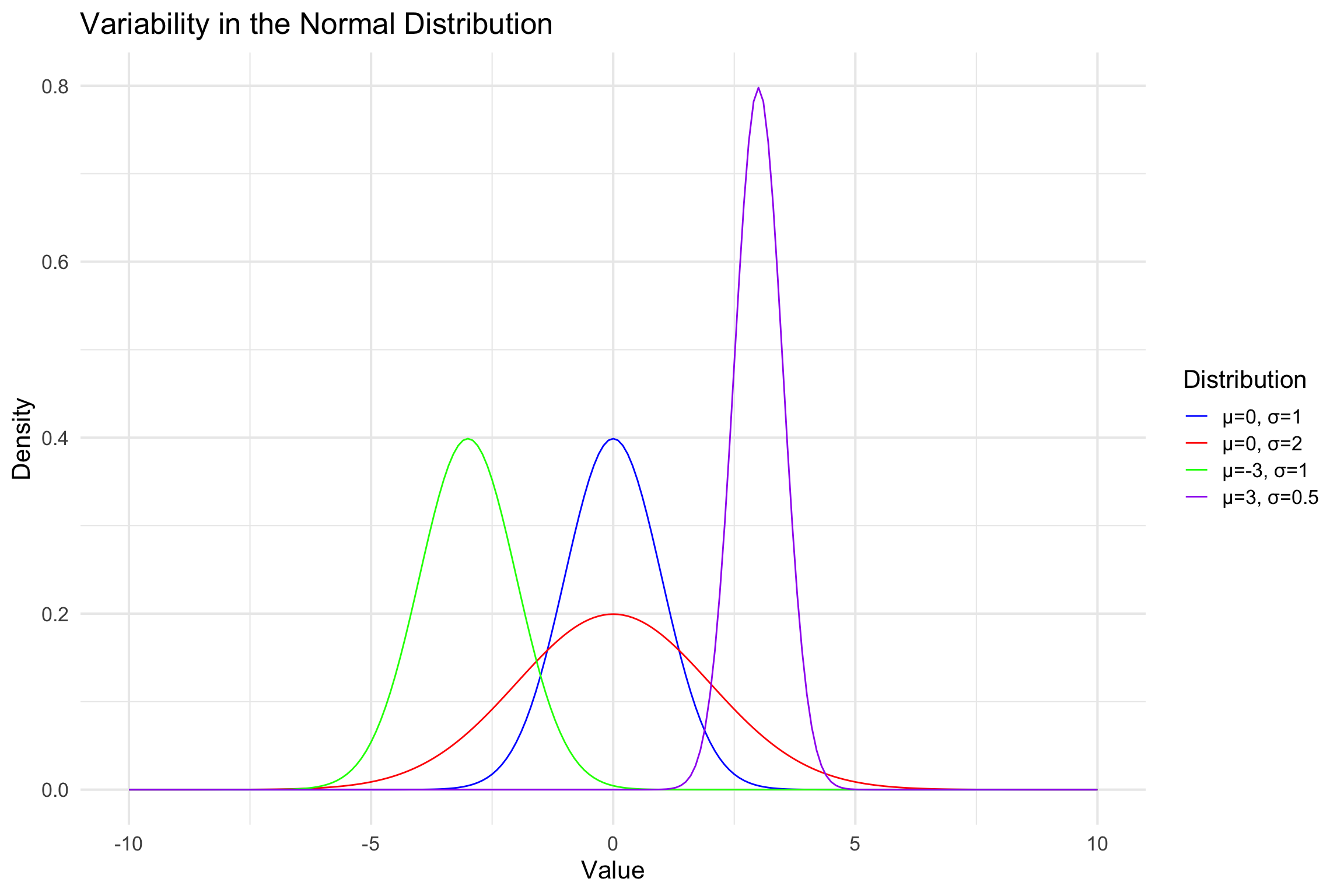
Normal distribution

Sometimes called a Gaussian distribution
If we assume a variable is at least normally distributed can make many inferences!
Most of the statistical models assume normal distribution
Error in linear models is assumed to distributed as normal

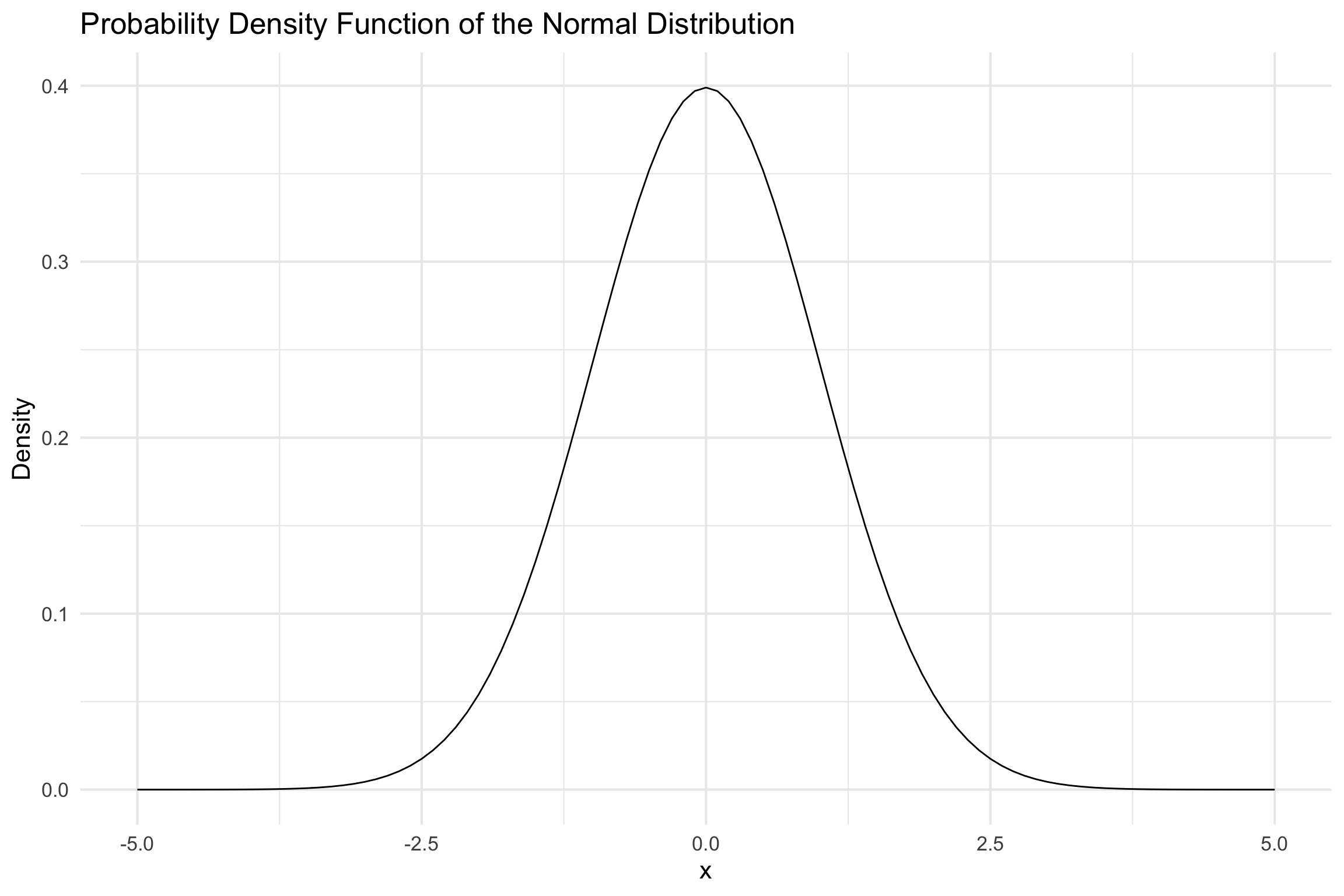
Normal distribution

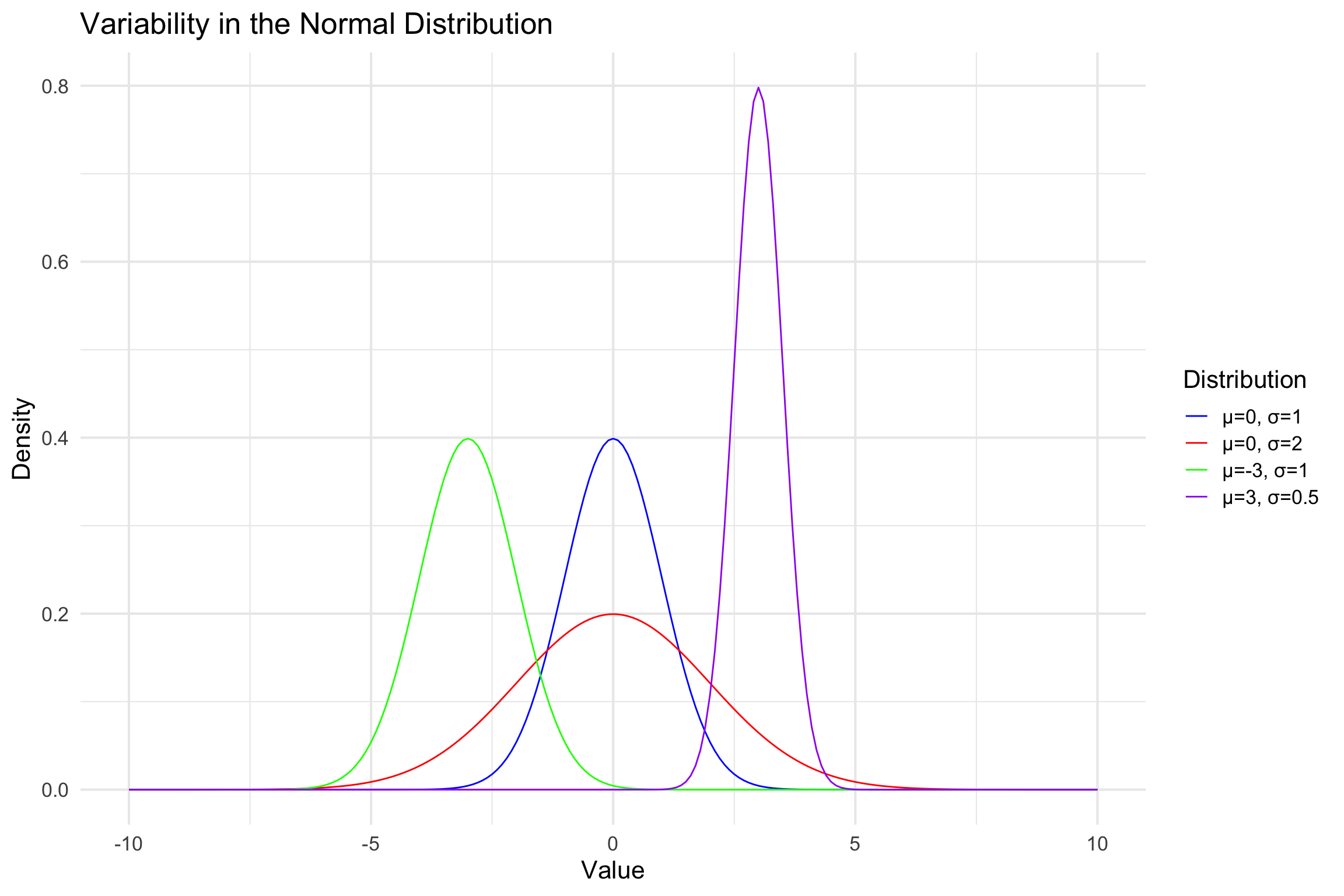
Normal(μ, σ)
- Parameters:
  - \(\mu\) = Mean
  - \(\sigma\) Standard deviation
    - On average, how far is each point from the mean (spread)?

Building a Model - Normal Distribution

Properties of a normal distribution
- Shape
  - Unimodal
  - Symmetric
  - Asymptotic

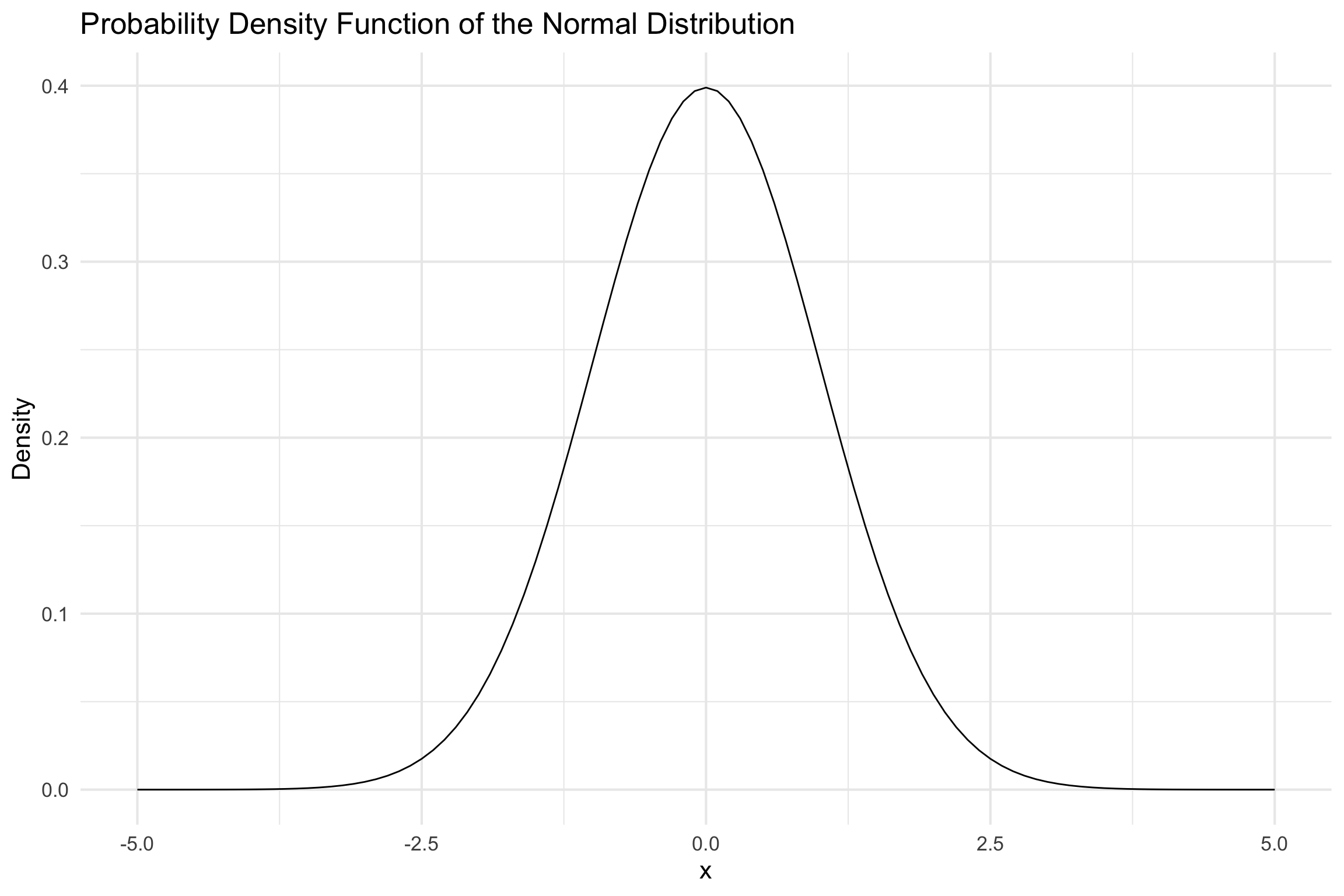
Building a Model - Normal Distribution

The PDF of a normal distribution is given by:

\(f(x) = \frac{1}{\sqrt{2\pi \sigma}}\exp\left[-\frac{(x-\mu)^2}{2\sigma^2}\right]\)

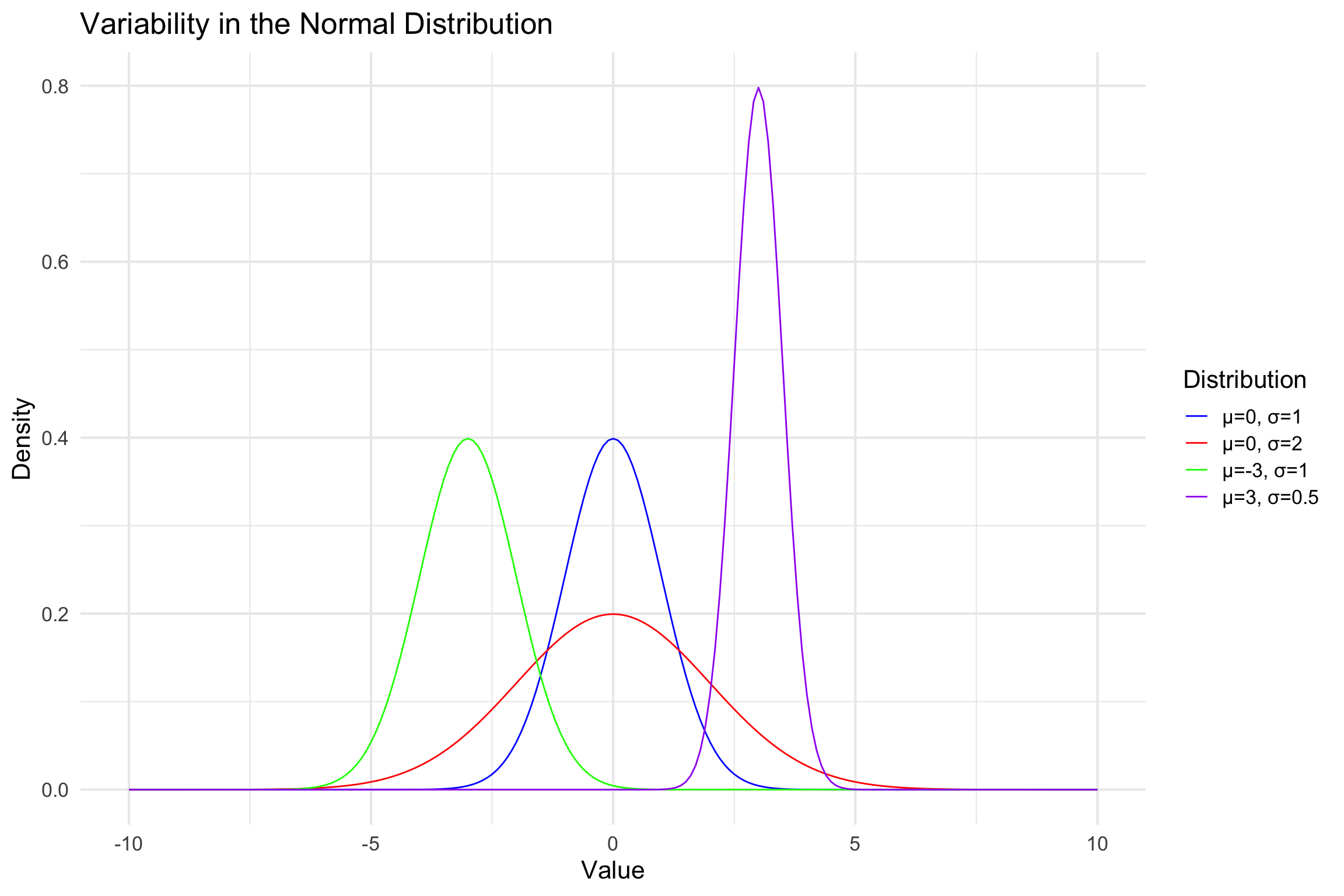
Normal Distribution

Skew

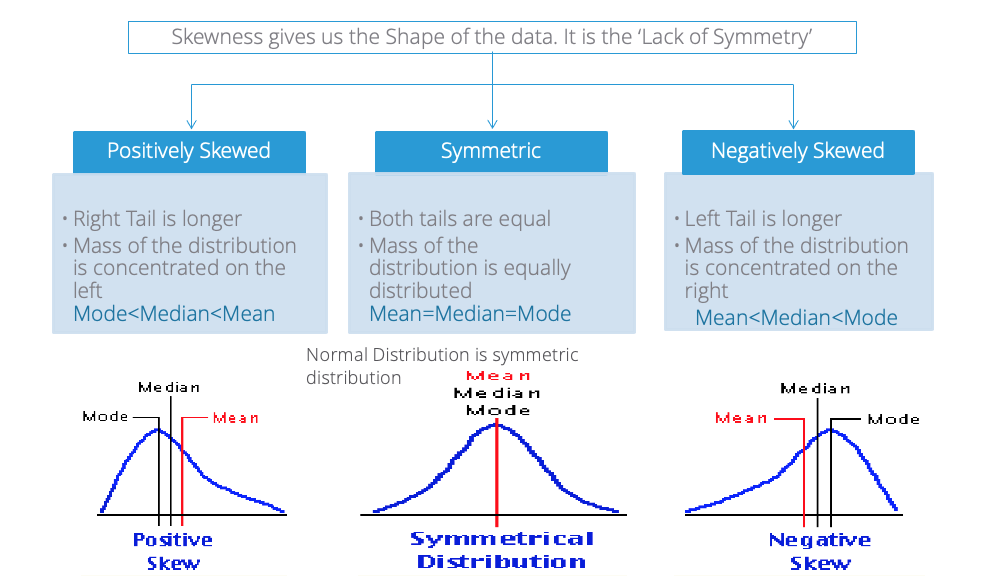
Normal Distribution

Peakedness

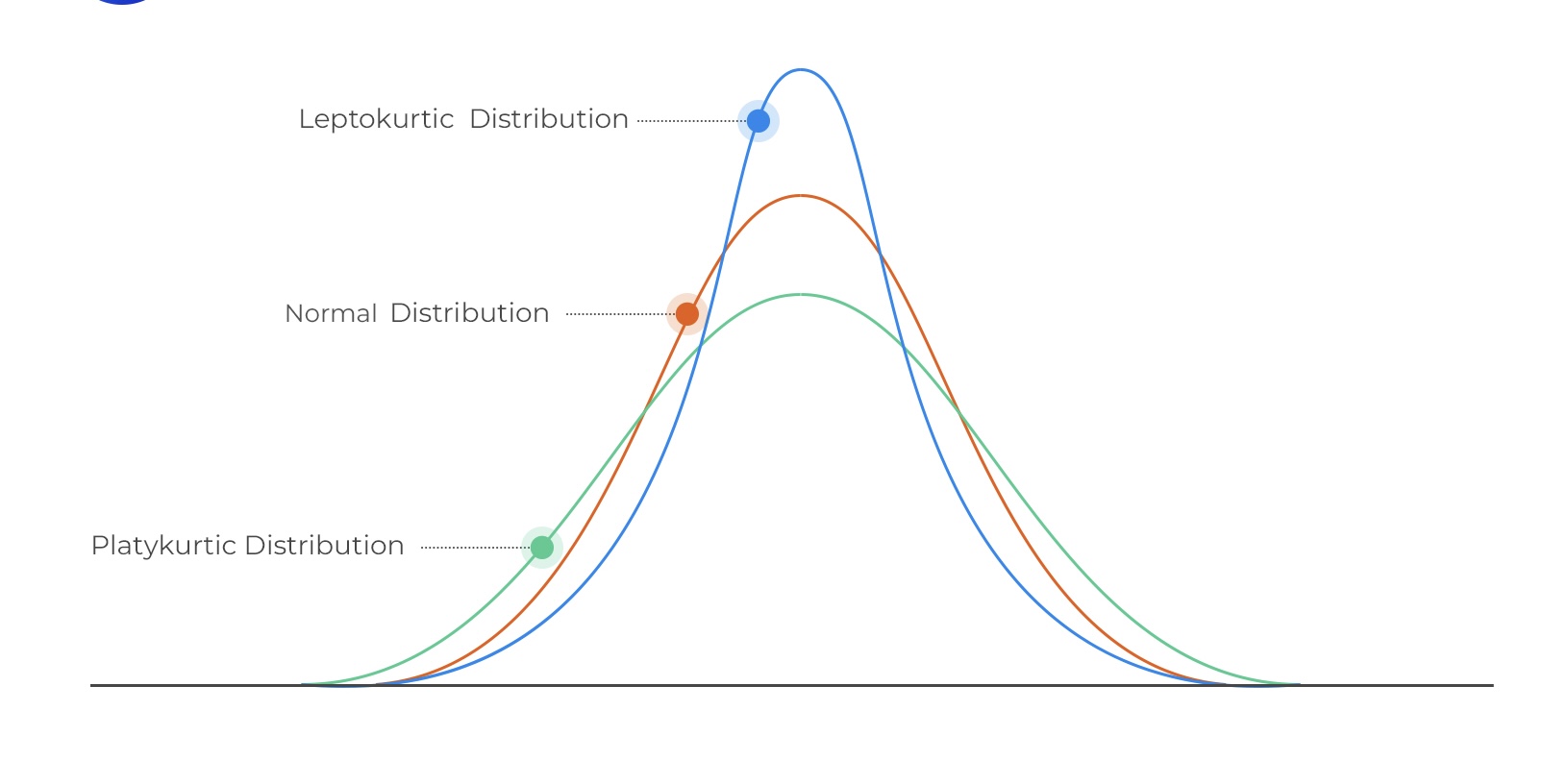
Normal Distribution

\(Y_1\) ∼ \(N(\mu, \sigma)\)
- \(Y_1\) ∼ Normal(100, 15)
- \(Y_2\) ∼ Normal(100, 15)
- \(Y_n\) ∼ Normal(100, 15)
Or for all observations,
- \(Y_i\) ∼ Normal(100, 15)

Normal Distribution

Everyone’s score comes from the same distribution
The average score should be around 100
Scores should be spread out by 15
Scores should follow bell-shaped curve

Probability and Standard Normal Distribution: Z-Scores

\[Z(x) = \frac{x - \mu}{\sigma}\]

Z-score /standard score tells us how far away any data point is from the mean, in units of standard deviation

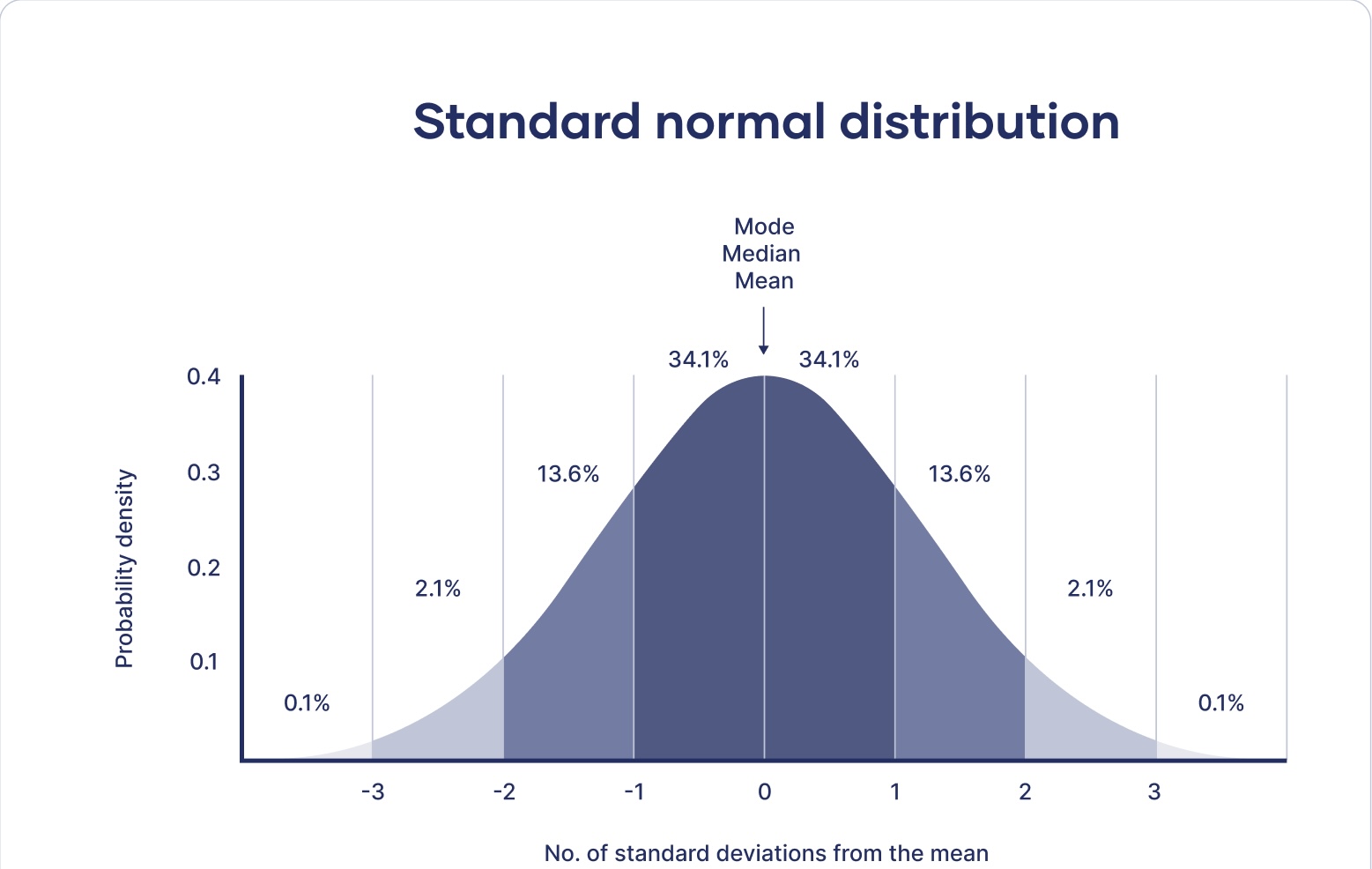
Standard Normal Distribution

Properties of standard normal
- Empirical Rule
  - 68.27% of the data falls within one standard deviation (sigma) of the mean
  - 95.45% falls within two sigma
  - 99.73% falls within three sigma

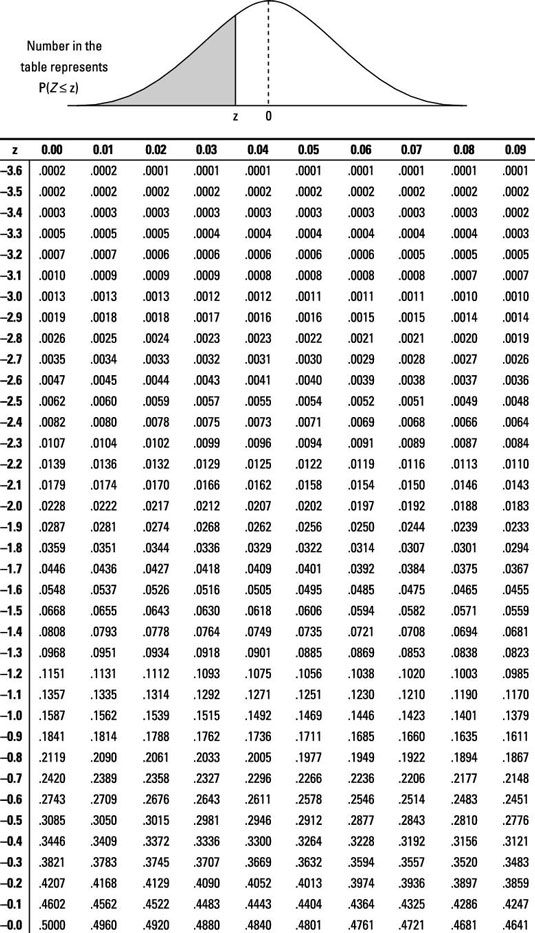
Z tables

NO MORE TABLES

Using R

dnorm() : Z-score to density (height) (PDF)
pnorm(): Z-score to area (CDF)
qnorm(): area to Z-score

Using R

pnorm function: Z-score to area (CDF)

\[ P(X <= x) \]

If you calculated a Z-score you can find the probability of a Z-score less than or equal (lower.tail=TRUE) or greater than (lower.tail=FALSE)

Using R: `pnorm`

mu <- 70
sigma <- 10
X <- 80

What is the z-score?

What percentage is below this z-score?

Above

Using R: `pnorm`

Calculate z-score

mu <- 100
sigma <- 15
X <- 55

Percentage below IQ score of 55?

Percentage above IQ score of 55?

Using R: `pnorm`

Percentage between IQ score of 120 and 159?

mu <- 100
sigma <- 15

Package `PnormGC`

Percentage between IQ score of 120 and 159?

library(tigerstats)

pnormGC(c(120,159), region="between" ,mean=100,sd=15, graph=TRUE)

[1] 0.09116933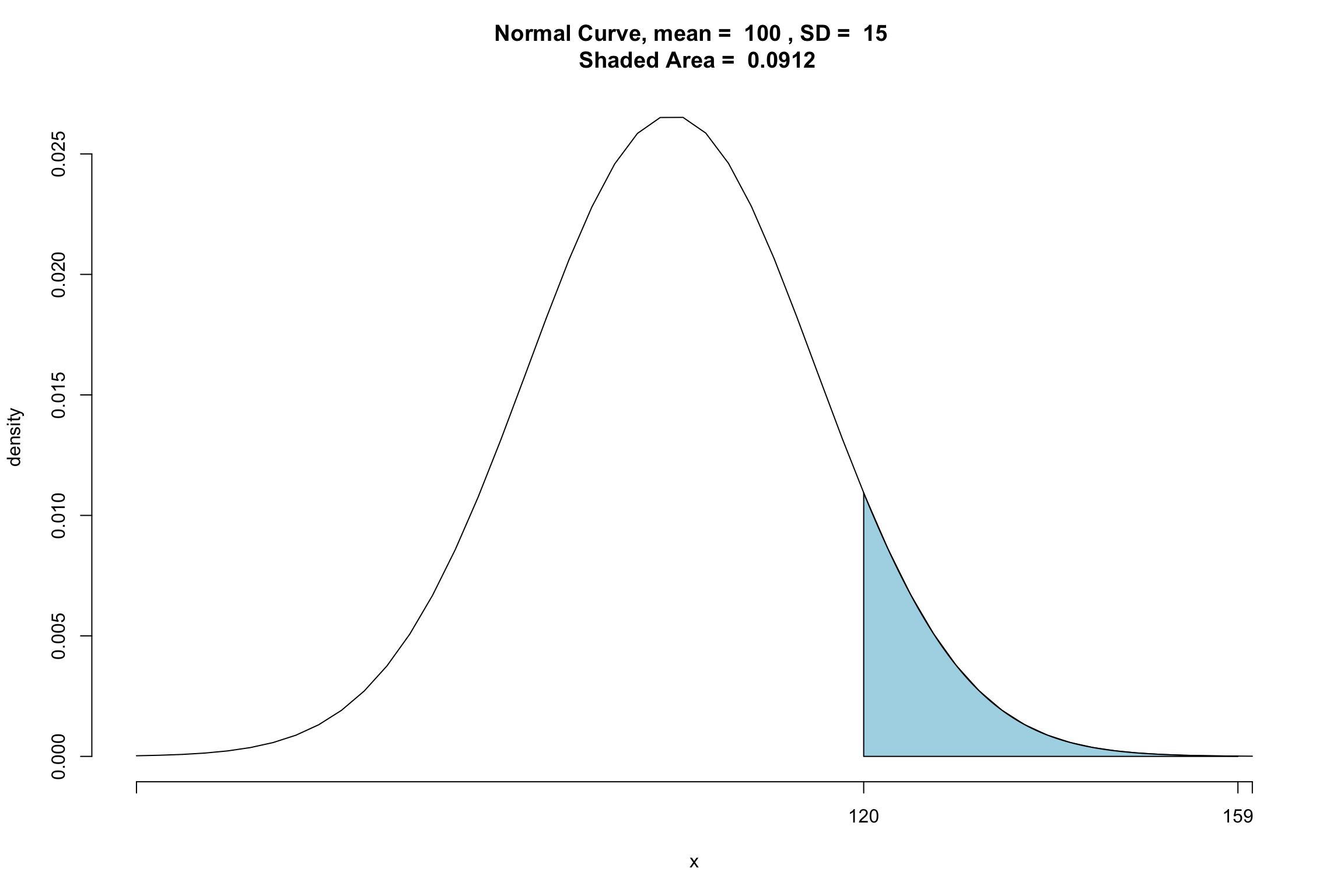

Package `PnormGC`

What about \(P(X \leq 69)\)

pnormGC(bound=69,region="below",
        mean=70,sd=3,graph=TRUE)

[1] 0.3694413

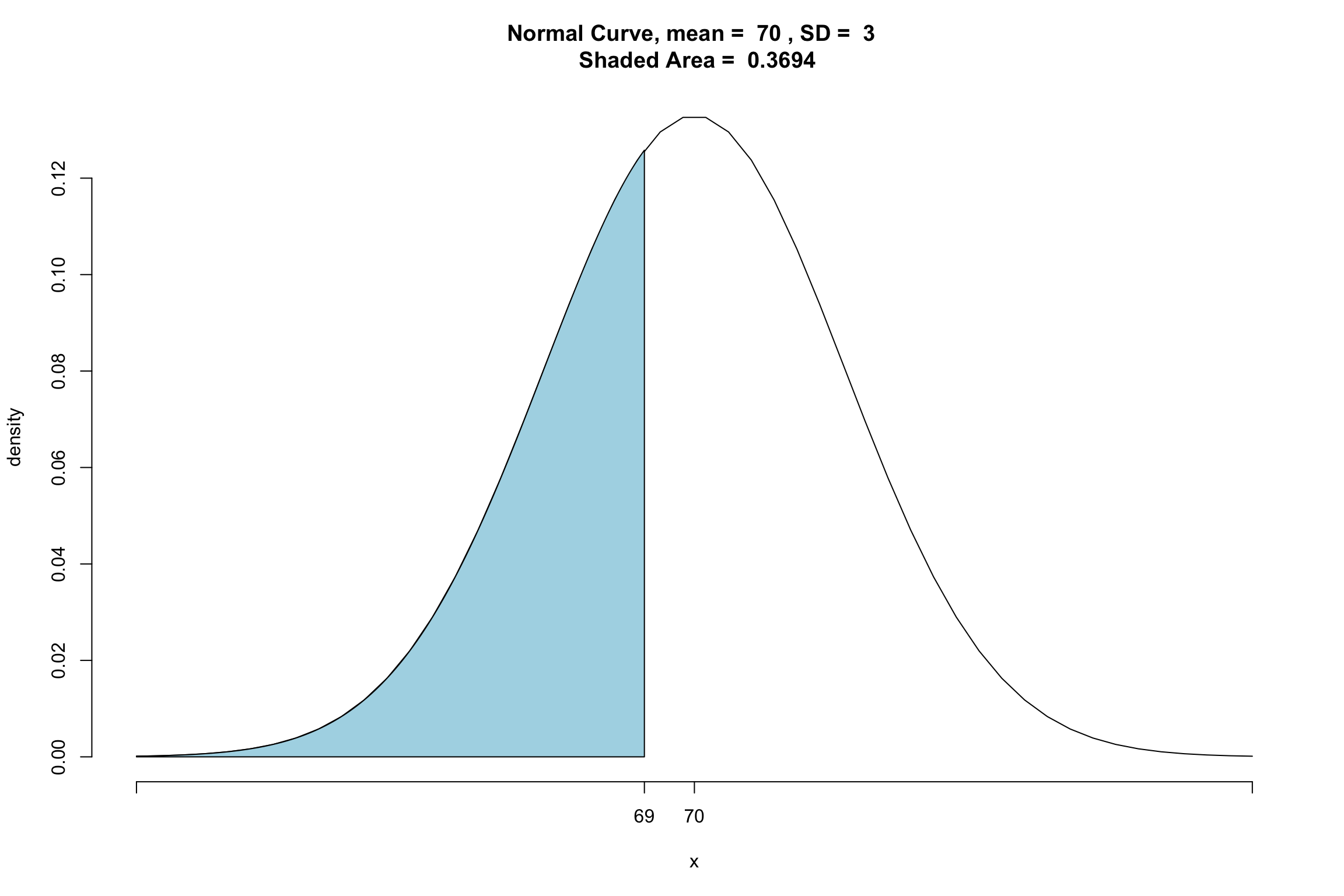
Using R: `qnorm`

qnorm(): area to z-scores
What is the score for which 5% lies above?

Practice `pnorm`

Suppose that BMI measures for men age 60 in a Heart Study population is normally distributed with a mean (μ) = 29 and standard deviation (σ) = 6. You are asked to compute the probability that a 60 year old man in this population will have a BMI less than 30.

What is the z-score?
What is the probability a 60 year old man in this population will have a BMI between 30 and 40?

Practice: `qnorm`

Suppose that SAT scores are normally distributed, and that the mean SAT score is 1000, and the standard deviation of all SAT scores is 100. How high must you score so that only 10% of the population scores higher than you?

Z-scores in practice

Standardization
- Scaling your measures so they are are comparable
- Does not change anything about the data!

library(easystats)
x=c(5, 6, 7, 8, 9, 10, 15, 16)
datawizard::standardize(x)

[1] -1.1150879 -0.8672906 -0.6194933 -0.3716960 -0.1238987  0.1238987  1.3628852
[8]  1.6106825
(center: 9.5, scale = 4)

Standardized Scores

A standardized score is a Z-score that has been transformed to have a \(\mu\) and \(\sigma\) different from standard normal
- IQ
  - \(\mu = 100\) \(\sigma = 15\)
- SAT
  - \(\mu =500\) \(\sigma = 100\)
- T-score
  - \(\mu = 50\) \(\sigma = 10\)
New score = new sd(Z) + New mean

Monsters, Models, and Normal Distributions

Announcements

Outline

Packages

What is a statistical model?

What is a model?

What is a model?

Distributions

Basic Structure of a Statistical Model

Models as Monsters

Statistical golems

Choosing a Statistical Model

Choosing a Statistical Model

The General Linear Model

The General Linear Model

A simple model

Building a Model - Notation

Building a Model - Notation

Building a Model - Notation

A simple model

A Simple Model: Data

Figuring out \(b_0\)

Types of Errors

Sum of errors (residuals)

Sum of absolute errors

Sum of squares (SS)

The mean

SSR minimized at mean

Describing error

Statistical Modeling: A Concrete Example

Building a Model - Concrete example

Building a Model - Concrete example

Building a Model - Concrete example

Building a model - Concrete example

Building a model - Concrete Example

Building a model - Concrete example

Building a model - concrete example

Building a model - Concrete example

A More Complex Model

What Makes a Model “Good”

Can a Model Be Too Good?

Normal distribution

Normal distribution

Normal distribution

Building a Model - Normal Distribution

Building a Model - Normal Distribution

Normal Distribution

Normal Distribution

Normal Distribution

Normal Distribution

Probability and Standard Normal Distribution: Z-Scores

Standard Normal Distribution

Z tables

Using R

Using R

Using R: pnorm

Using R: pnorm

Using R: pnorm

Package PnormGC

Package PnormGC

Using R: qnorm

Practice pnorm

Practice: qnorm

Z-scores in practice

Standardized Scores

Using R: `pnorm`

Using R: `pnorm`

Using R: `pnorm`

Package `PnormGC`

Package `PnormGC`

Using R: `qnorm`

Practice `pnorm`

Practice: `qnorm`