Statistical Inference: Populations, Sampling Distributions, and Uncertainty

Princeton University

Author

Jason Geller, PH.D.(he/him)

Published

October 3, 2023

Where are we going?

  • Today:

    • Sampling distributions
    • Uncertainty (confidence intervals, margin of error)

  • Monday:

    • Null hypothesis significance testing (p-values, null hypotheses)

Packages










Population




Entire collection of units interested in studying




    

  • Clearly defined
    • 

  • Typically large
    • 

















Sample




Smaller subsets of population


















Statistical Inference


















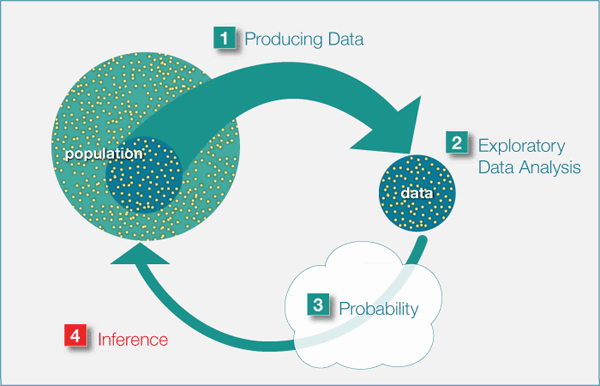
Estimation


    

  • Parameters and Statistics
    

      

    • Parameter
      

        

      • Characteristics of the population
        • 

      • 

    • Statistics: Estimates of population parameters
      

        

      • This is a random variable! We can create a sampling distribution from this
        • 

      • 

    • 











Activity - Sampling Distributions


There is a large bowl of balls that contains red and white balls. Importantly, we know that 37.5% of the balls are red


What proportion of this bowl’s balls are red?


    

  1. Pull a random sample of 10 5x
    2. 

  2. Tell me how many of reds you pulled from each sample (prop)
    

    3. 







  









Activity - Sampling Distributions






  









Activity - Sampling Distributions


There is a large bowl of balls that contains red and white balls. Importantly, we know that 37.5% of the balls are red


What proportion of this bowl’s balls are red?


    

  1. Pull a random sample of 50 5x
    2. 

  2. Tell me how many of reds you pulled (prop)
    

    3. 







Activity - Sampling Distributions






  









10,000 times






  









10,000 Times




ggplot(virtual_prop_red, aes(x = prop_red)) +
  geom_histogram(binwidth = 0.05, boundary = 0.4, color = "white") +
  geom_vline(xintercept =.37, colour="green", linetype = "longdash")+
  labs(x = "Proportion of 50 balls that were red", 
       title = "Distribution of 10,000 proportions red") 








Key points


    

  • Two samples from the same population will tend to have somewhat different means
    

      

    • Conversely, two different sample means does NOT mean that they come from different populations
      • 

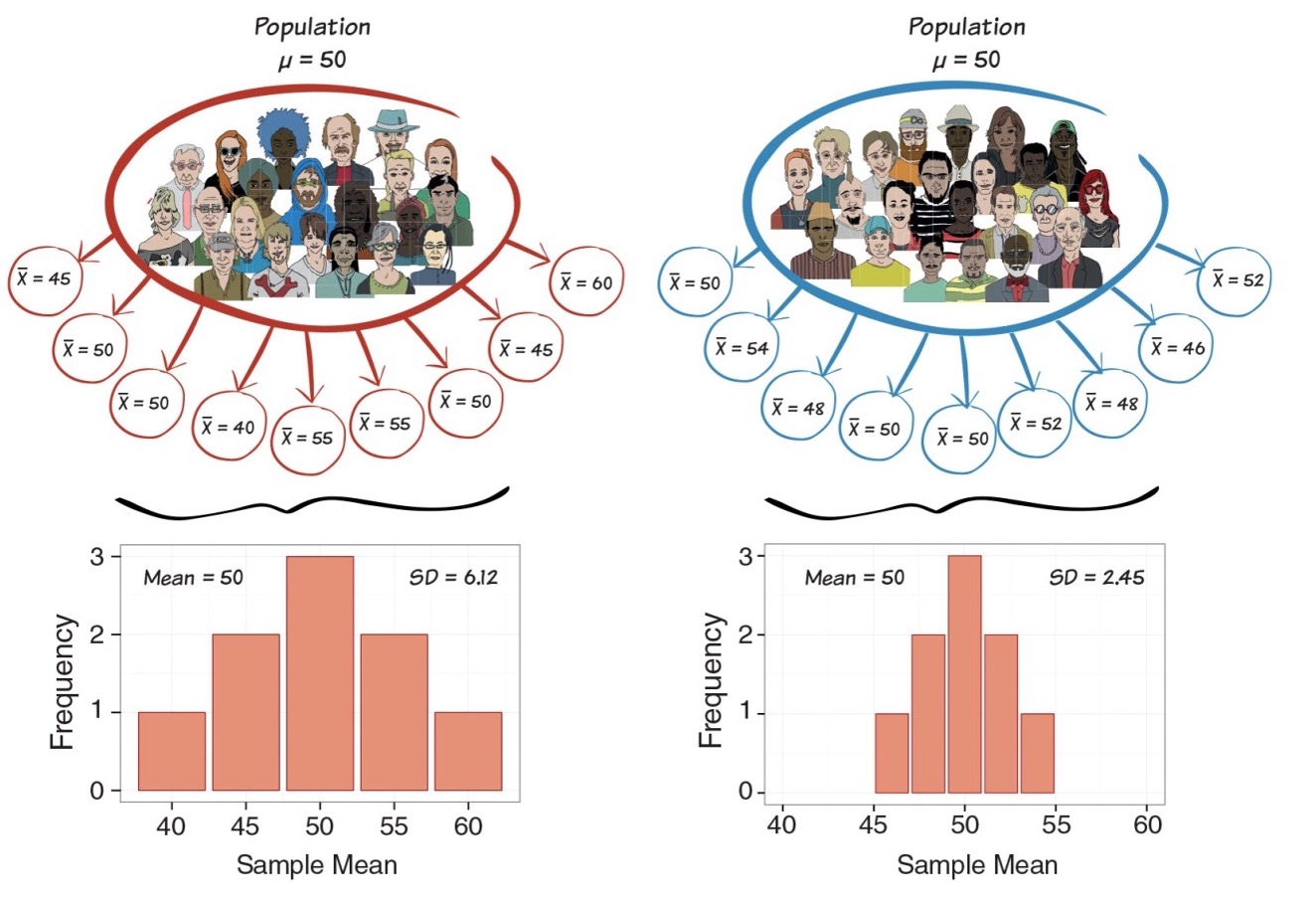
    • The variance of the sampling distribution of means gets smaller as the sample size increases
      • 

    • Mores samples give better estimate of population mean
      • 

    • 







Sampling Distribution


    

  • The probability distribution of a given statistic (e.g., mean) taken from a random sample
    

      

    • Distribution of statistics (e.g., mean) that would be produced in an infinite repeated random sampling (with replacement) (in theory)
      • 

    • 

  • IMPORTANT: Can be any statistic (proportion, mean, standard deviation)
    • 







Constructing Sampling Distribution


    

  1. Randomly draw n sample points from a finite population with size N
    2. 

  2. Compute statistic of interest
    3. 

  3. List different observed values of the statistic with their corresponding frequencies
    4. 







Properties of Estimators


    

  • Unbiased
    

      

    • Parameter value = estimate from sampling distribution
      • 

    • 

  • Efficient
    

      

    • More precise
      • 

    • 

  • Consistency
    

      

    • Sampling distribution becomes narrower if we increase sample size
      • 

    • 







Example: Sampling Distribution of the Mean


    

  • Scores on a statistics test
    • 









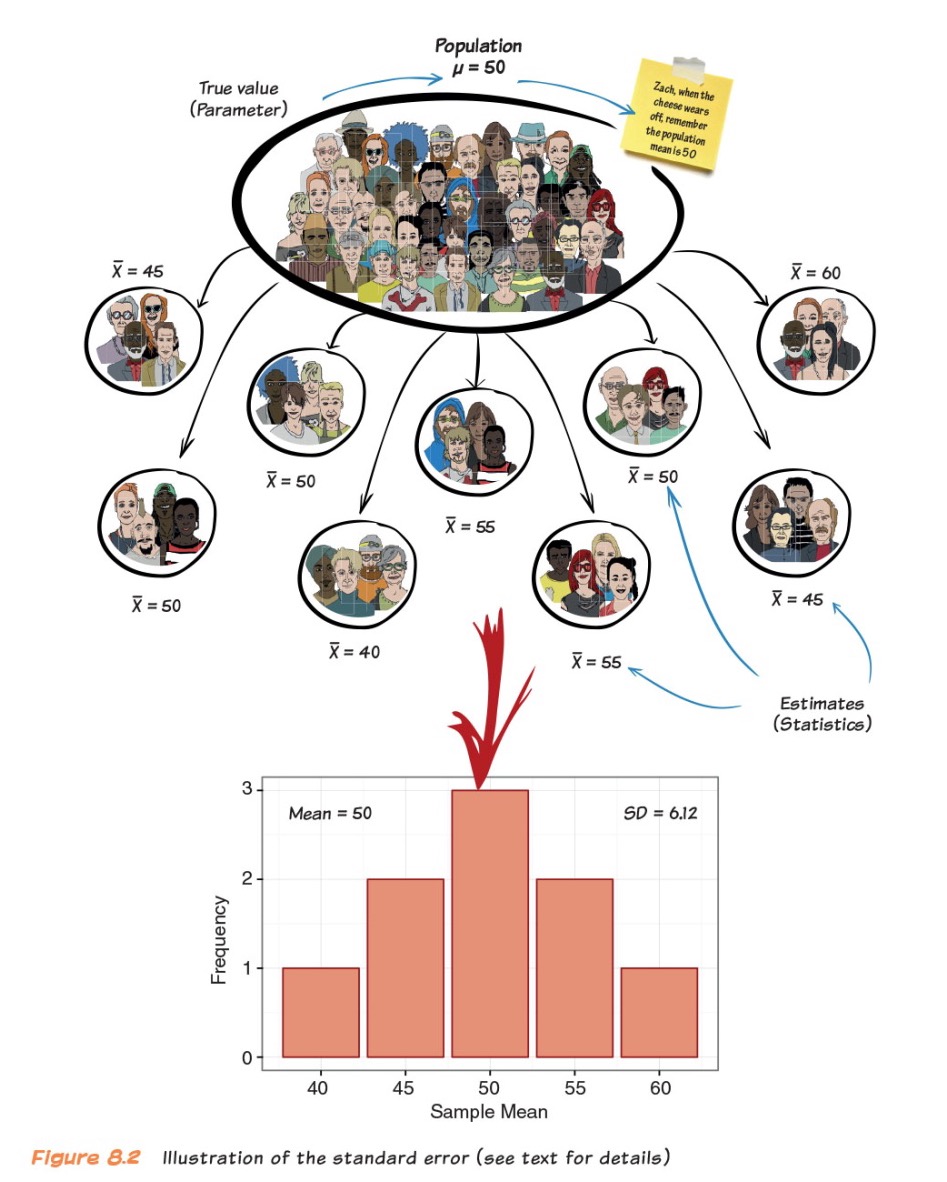
Taken from Andy Field’s “Adventures in Statistics”










Sampling Error (Standard Error)








Sampling Error (Standard Error)


    

  • How certain are we that our estimate represents the mean of the population?
    

      

    • Say it with me: The standard deviation of the sampling distribution is the standard error
      • 

    • It tells us how much variability there is between sample estimate and population parameter
      • 

    • 



\[SEM = \sigma/\sqrt(N)\]






SEM


    

  • What does smaller SEM tell us about our estimate?

      

    • Estimate is likely to be closer to population mean
      • 

    • 

















Sampling Distributions












Note







Sampling distributions are theoretical, and the researcher does not select an infinite number of samples. Instead, they conduct repeated sampling from a larger population, and use the central limit theorem to build the sampling distribution










A Tale of a Theorem and a Law: Magic


    

  • Central Limit Theorem
    

      

    • Properties:
      

        

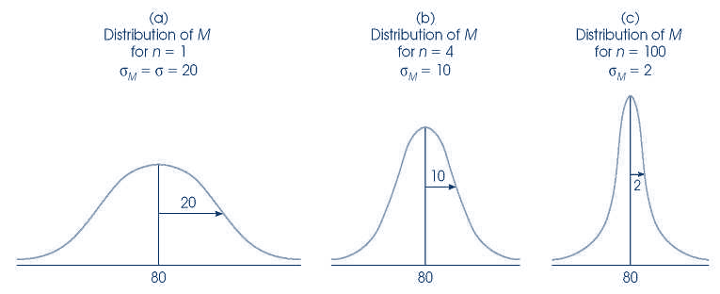
      1. The distribution of the sample mean approaches the normal distribution as the sample size increases
        2. 

      2. The standard deviation of the sampling distribution will be equal to the SD of the population divided by the square root of the sample size. s= \(\sigma/\sqrt(n)\)
        3. 

      • 

    • 



Important: about the shape of distribution






Central Limit Theorem


    

  • Why is the Central Limit Theorem so important to the study of sampling distribution?
    

      

    • Kicks in regardless of the distribution of the random variable
      • 

    • We can use the normal distribution to tell us how far off our own sample mean is from all other possible means, and use this to inform decisions and estimates in null hypothesis statistical testing
      • 

    • 







Central Limit Theorem


Certain conditions must be met for the CLT to apply:


    

  • Independence: Sampled observations must be independent. This is difficult to verify, but is more likely if
    

      

    • Random sampling / assignment is used
      • 

    • 

  • Sample size / skew: Either the population distribution is normal, or if the population distribution is skewed, the sample size is large (> 30)
    

      

    • The more skewed the population distribution, the larger sample size we need for the CLT to apply
      • 

    • 







Real Data




data("gapminder", package = "dslabs") 
gapminder_2015 <- gapminder %>% 
  filter(year == 2015, !is.na(infant_mortality))
ggplot(gapminder_2015) +
  geom_histogram(aes(x = infant_mortality), color = "black")  +
  xlab("Infant mortality per 1,000 live births") +
  ylab("Number of countries")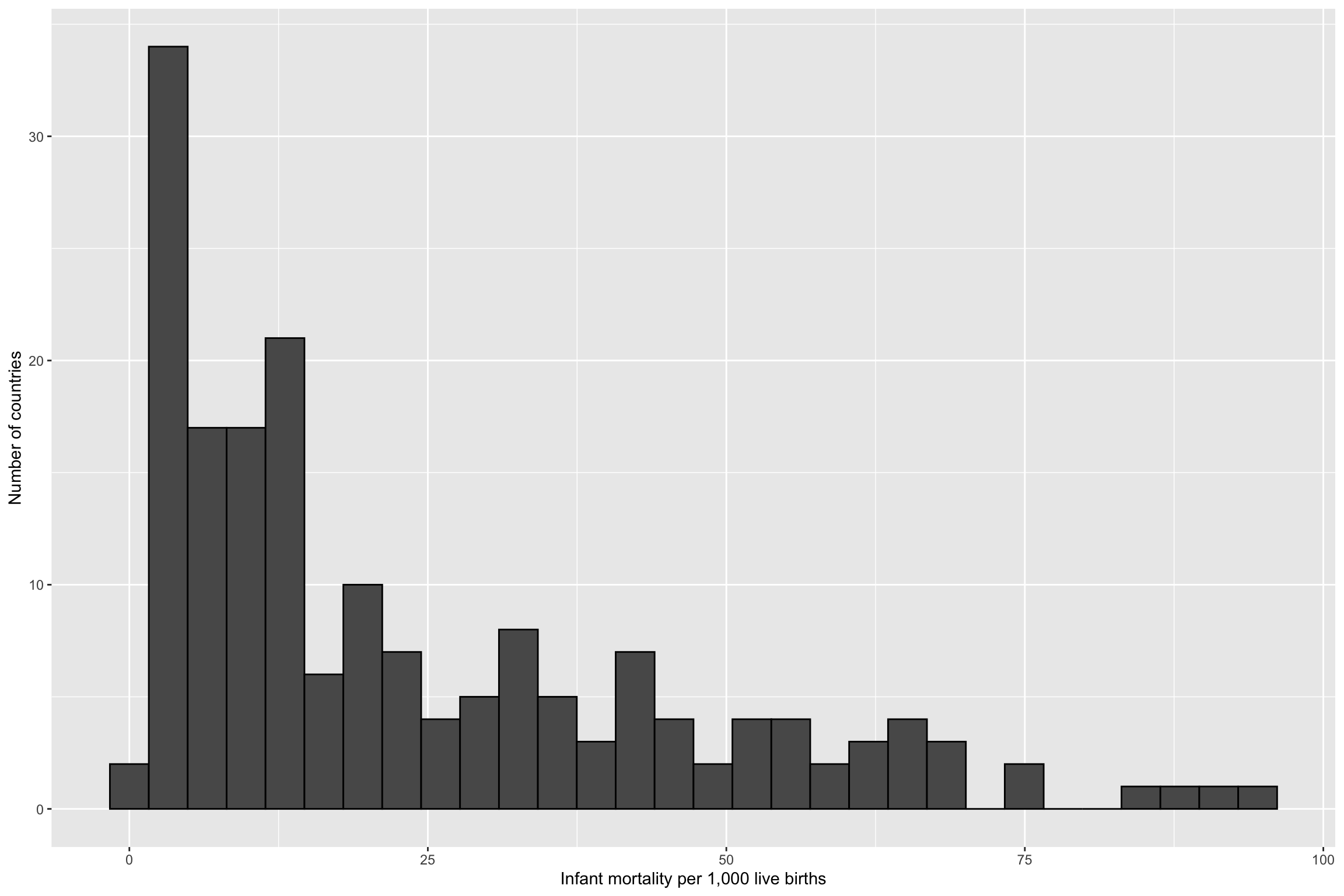


























R Simulations




library(infer)
library(cowplot)

sample_5 <- rep_sample_n(gapminder_2015, size = 5, reps = 10000) %>% 
  group_by(replicate) %>% 
  summarise(mean_infant_mortality = mean(infant_mortality)) %>% 
  mutate(n = 5)

sample_30 <- rep_sample_n(gapminder_2015, size = 30, reps = 10000) %>% 
  group_by(replicate) %>% 
  summarise(mean_infant_mortality = mean(infant_mortality)) %>% 
  mutate(n = 30)

sample_100 <- rep_sample_n(gapminder_2015, size = 100, reps = 10000) %>% 
  group_by(replicate) %>% 
  summarise(mean_infant_mortality = mean(infant_mortality)) %>% 
  mutate(n = 100)

all_samples <- bind_rows(sample_5, sample_30, sample_100)








Larger N Equates Better Normal Approximation
























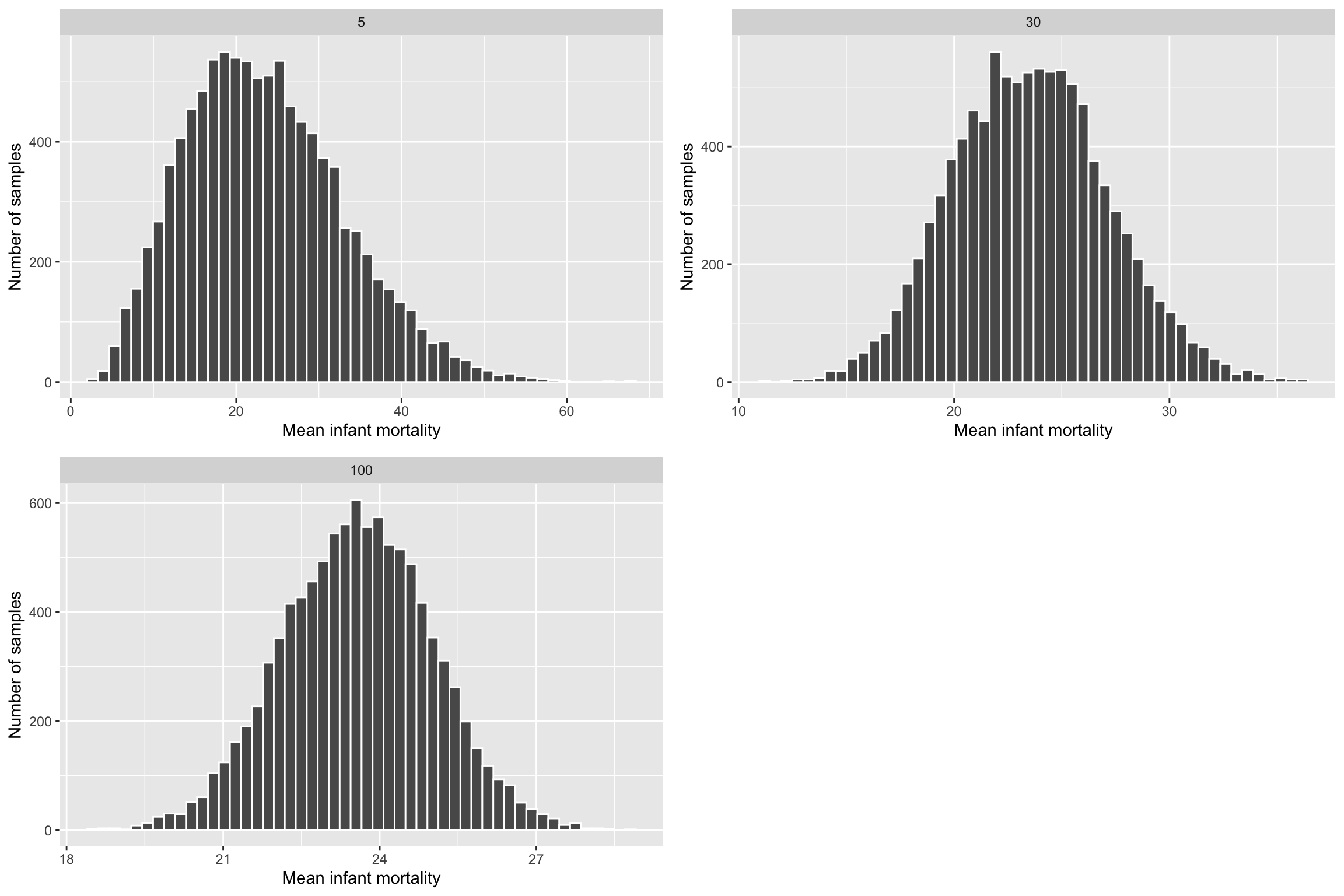
Law of Large Numbers


    

  • Law of large numbers (LLN)
    

      

    • Implies that sample average \(\bar{X_n}\) will better approximate \(\mathbb{E}[X]\) as sample size increases
      • 

    • 

  • Super powerful: can be applied in most settings without knowledge of the underlying probability distribution
    • 

  • The Law of Large number justifies the use of Monte Carlo simulations
    

      

    • Repeat simulation trials many many times and take the mean of these trials
      • 

    • 



IMPORTANT: about the mean






Measuring Uncertainty




From a point estimate to an interval


    

  • Mean and SEM are point estimates
    • 

  • What if we could create an interval that we are “reasonably confident” contains the true population mean?
    • 







Estimation Error and MOE


    

  • MOE (margin of error)
    

      

    • Largest likely estimation error
      • 

    • 



\[MoE = 1.96 X SE\]


    

  • Where did 1.96 come from?
    • 







Estimation Error and MOE
















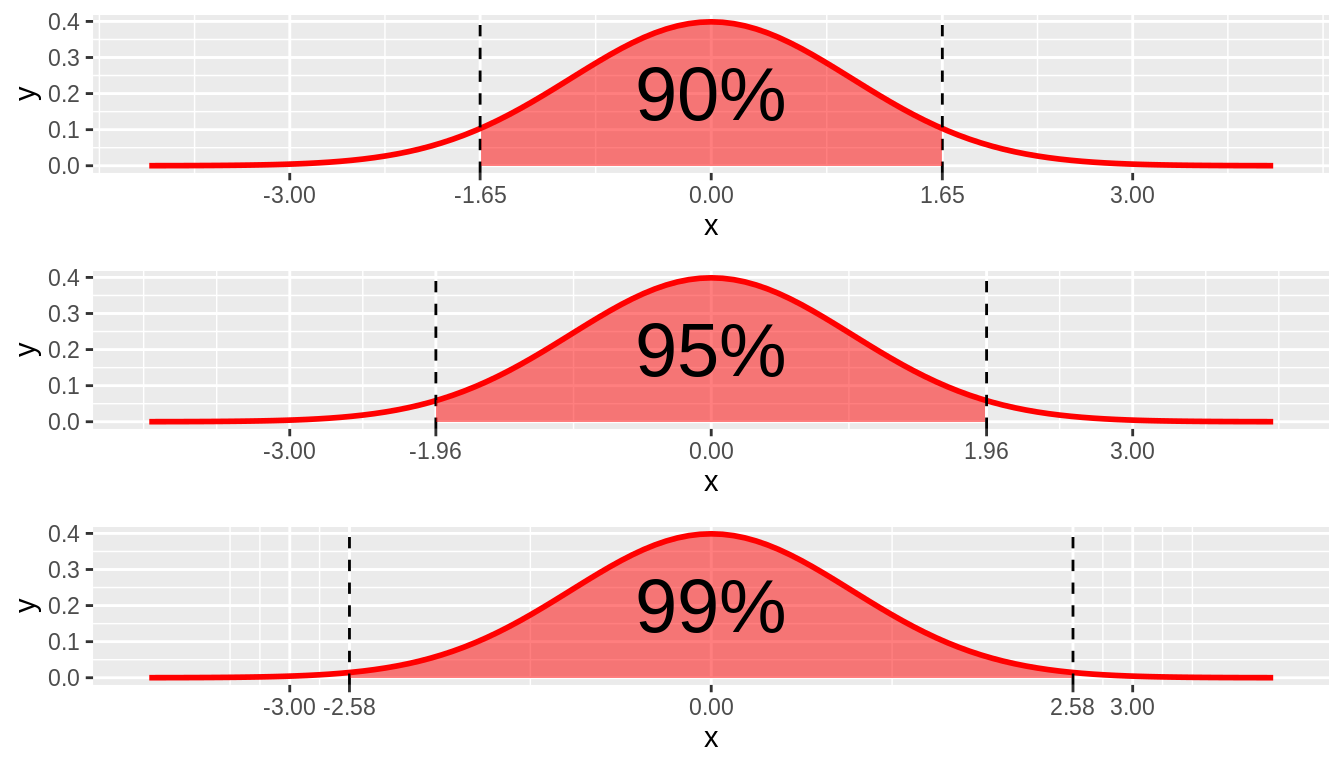
Combining Estimates Precision






    

  • CIs
    

      

    • Range of values that are likely to include the true value of the parameter
      • 

    • Allows us to provide point estimate with precision (SE)
      • 

    • 























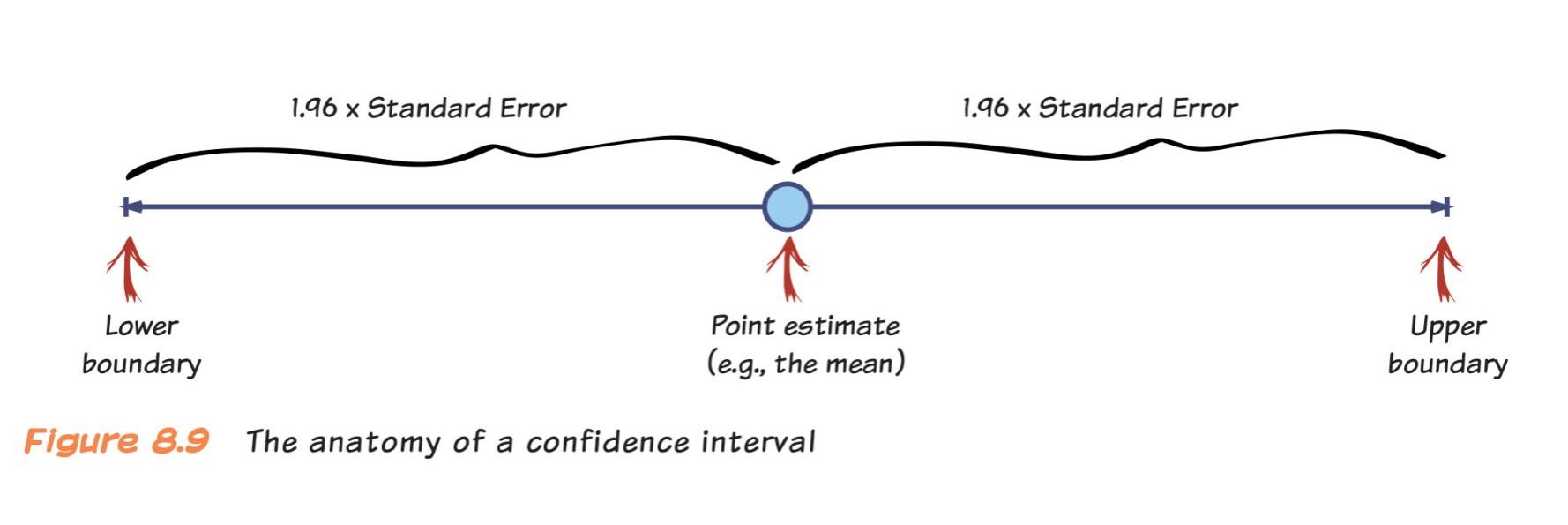
Anatomy of a Confidence Interval




Public support for Proposition A is 53%




    

  • 53% support, 95% CI [51, 55]
    • 

















CIs - Activity


https://seeing-theory.brown.edu/frequentist-inference/index.html#section2


    

  • Start with a normal distribution to sample from
    • 



    

  1. How do the lengths of the confidence intervals change with sample size?
    2. 

  2. With confidence level?
    3. 







CIs


    

  • Sample size
    • 

















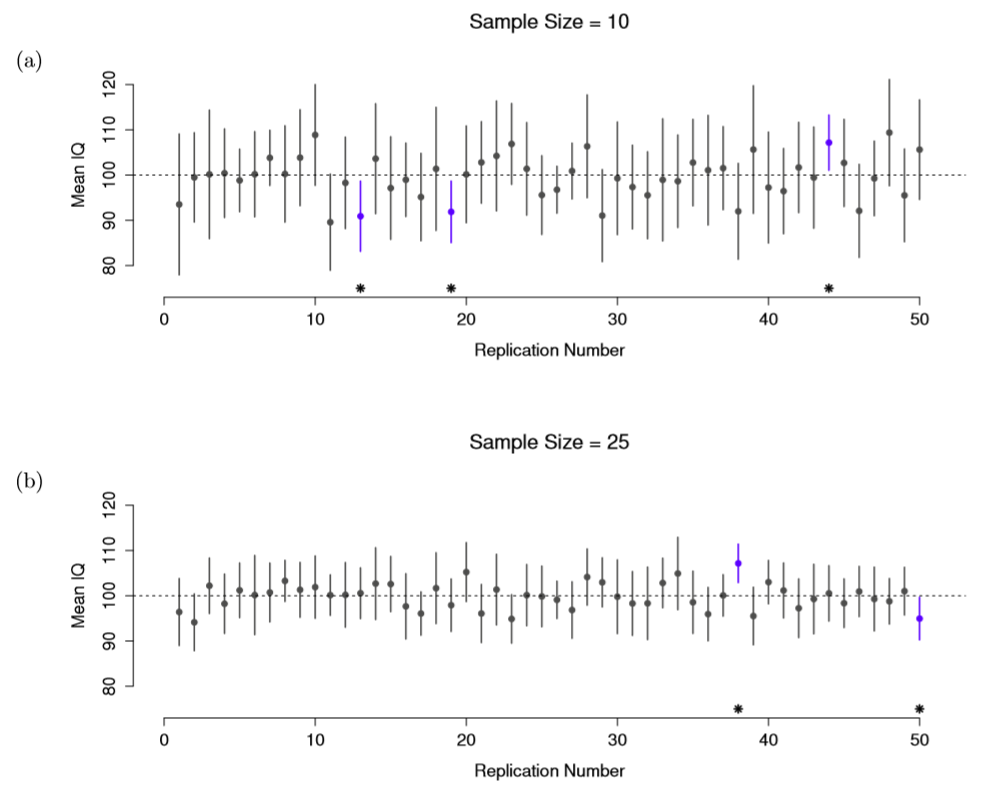
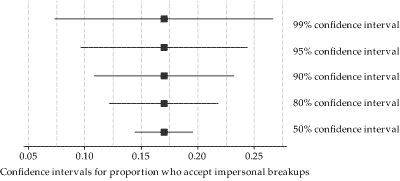
CIs






    

  • 95 is referred to as confidence level
    

      

    • i.e., How confident CI includes \(\mu\)
      • 

    • 

  • Does not only have to be 95!
    

      

    • Greater C = longer CI
      • 

    • 























How to Calculate CIs


1. Calculate the estimate from your sample


2. Calculate the standard error of your estimate


3. Determine the appropriate sampling distribution for your standardized estimate (e.g., normal)


    

  1. Determine your desired level of confidence (e.g. 90%, 95%, 99%)
    2. 



    

  • Lower boundary = estimate - MoE (1.96 X **SE**)
    • 




    

  • Higher boundary = estimate + MoE (1.96 X **SE**)
    • 



\[
\bar{x} \pm 1.96 \dfrac{\sigma}{\sqrt{n}}.
\]






CI Interpretations




There is a 95% probablity that our interval includes the true population mean




. . .


    

  • Nope! Frequentist CIs are often misinterpreted
    • 







CI Interpretations


    

  • https://seeing-theory.brown.edu/frequentist-inference/index.html#section2
    • 



    

  1. CI dance: One from the dance (most likely captures the parameter we are estimating, but it could not)
    

      

    • General interpretation: They tell us if I collected a 100 samples in an identical way, and for each of them calculated the mean and CI, then we would expect 95% of these samples to contain true mean
      • 

    2. 







CI Interpretations


2. Precision: MoE gives us a sense of precision


    

  1. Prediction: CIs give useful information about replication
    2. 



    

  • E.g., If a replication is done, 83% chance (5 in 6 chance) 95% CI will capture the next mean
    • 



1






CIs and P-values












Note







We can use CIs to test the significance of the effect. If they do not include 0, we can usually say p < .05










What do we do when $\sigma$ unknown?


    

  • USE \(s\) - SD of the sample
    • 



\[
Z(x) = \frac{x - \mu}{\sigma}
\]


\[s = \sqrt{\frac{1}{N-1} \sum_{i=1}^N (x_i - \overline{x})^2}\]






The \(t\) Distribution


    

  • Small samples: more conservative test
    • 

  • t-distribution has fatter tails
    • 

  • Coverage is more conservative
    • 























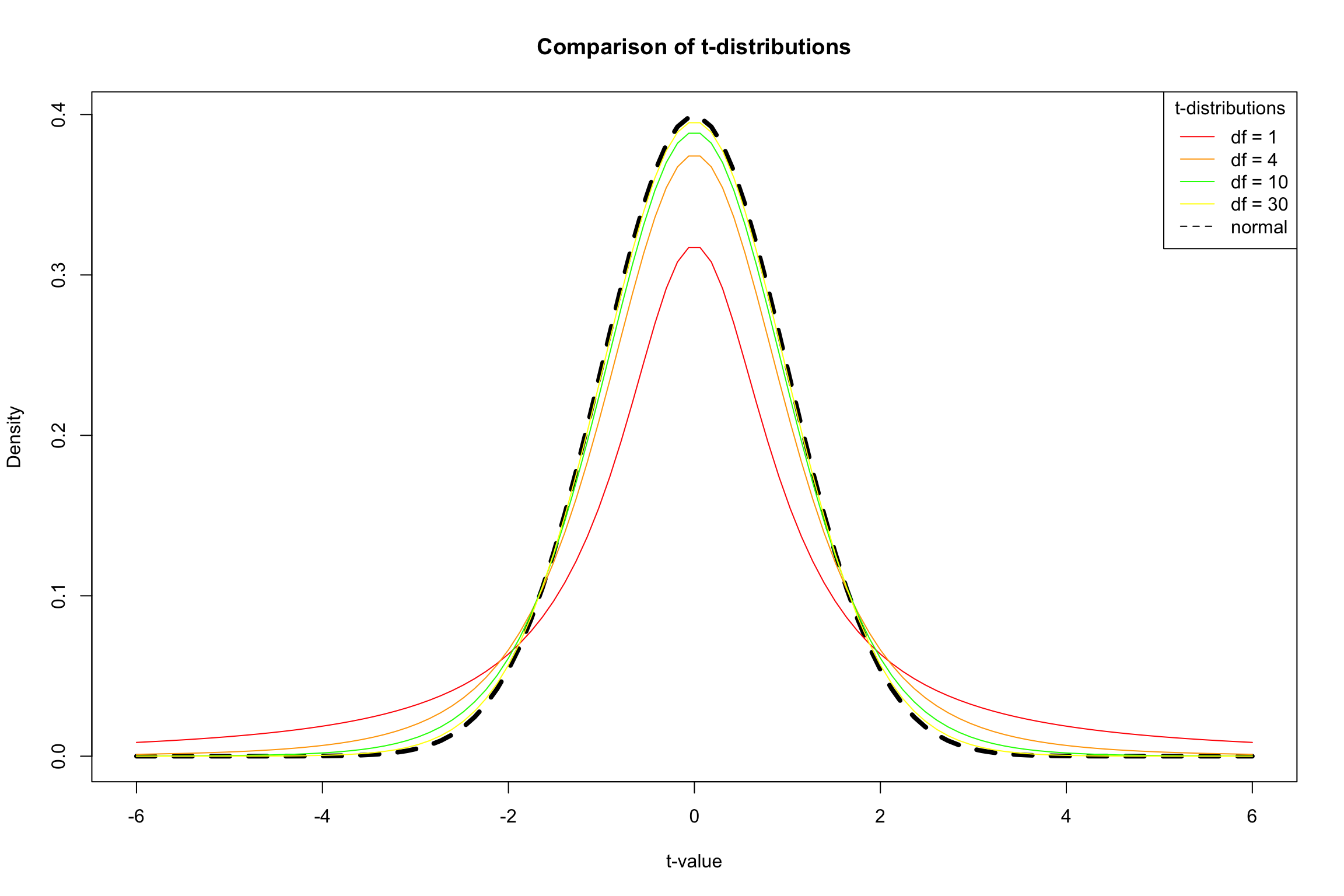
N-1 is non-biased (not going to concern ourselves with the proof). We are taking sample SD instead of pop SD. It is going to be biased if we dont.








Degrees of Freedom


    

  • df = (N-1)
    • 

  • What is DF you ask?
    

      

    • Number of separate independent pieces that can vary
      • 

    • 









Calculating CIs for \(t\)


\[
MoE = t_.95(df) \times s/\sqrt(N)
\]






  









Candy Experiment Revisited


    

  • Let’s calculate a confidence interval for the candy experiment
    • 







  









Candy Experiment Revisited


    

  • Empty model
    • 







  









Candy Experiment Revisited


    

  • Let’s get the means for each condition
    • 







  









Candy Experiment Revisited


    

  • Let’s calculate our CIs
    • 







  









Write-up


    

  • 95% CI [lower, upper]
    • 





People who completed the statistics test scored *M* = 75.00, 95% CI [70, 80], which was higher than those who completed it as themselves, *M*= 50.00, 95% CI [35, 65].








Summary


    

  • Confidence intervals quantify uncertainty about our estimates of the population mean based on a sample
    

      

    • Captures precision of the sampling process, not about our beliefs about the value of the true population parameter
      • 

    • 

  • Encourages thinking about plausible range of values instead of a point estimate
    • 

  • Larger samples, populations with smaller variances, and lower confidence levels lead to smaller intervals
    • 











Footnotes



    

  1. Cumming & Calin-Jageman: Introduction to the New Statistics↩︎
    2.