04-Probablity Distributions and Visualization Notes

Princeton University

Outline

• Probability - what is it?

• Random processes and variables

• Probability distributions

• DGP

• ggplot primer

• Visualizing variance

Probability warm-up

1. What is probability of drawing the ace of spades from a fair deck of cards?

2. What is the probability of drawing an ace of any suit?

3. You are going to roll some dice twice. What is the probability you roll doubles?

4. What is the chance that a live specimen of the New Jersey Devil will be found?

5. Who is more likely to be a victim of a street robbery, a young man or an old woman?

Frequentist interpretation of probability

• Classical statistical inference is based off this interpretation

• The frequentist approach treats probabilities as relative frequencies

  • If we say that the probability of rolling a 5 on a fair die is 1/6, we mean that, if the die were rolled an infinite number of times, 1/6 of all rolls would be a 5

What probability is not

What is probability theory?

• Probability is the study of random processes

  • Probability is used to characterize uncertainty/randomness

    

Random processes: intuition

• Let’s flip a fair coin

1. Can you tell me what the outcome will be?

2. If we were to flip a fair coin many many times, would you be able to tell the proportion of times that we would obtain heads?

. . .

• If answer to first question is “NO” AND Answer to second question is “YES”
  • You are dealing with a random process

Random processes

• Random processes are mechanisms that produce outcomes… from a world/set of possible outcomes… with some degree of uncertainty but with regularity

. . .

• Random assignment in experiments

. . .

• Random dram of a sample of n individuals from a population of N individuals

. . .

• Rolling a die

What is a random variable?

• A variable that depends on a random process

  • Think about the following random phenomenon: “randomly selecting 2 students in this class room”

    • Sample space?

      • One possible outcome: \(\omega = \{\mathrm{Ari, \: Alex}\}\)

      • Another possible outcome: \(\omega = \{\mathrm{Kennedy, \: Brooke}\}\)

What is a random variable?

• Can this be considered a random variable?

. . .

• No. Random variables are always numeric

• We operate on random variables using math

Illustration

• Random variables are mappings from events to numbers

• Formally, a random variable is defined as a function that maps the sample space \(\Omega\) of a random generative process into the real line (or into real numbers)

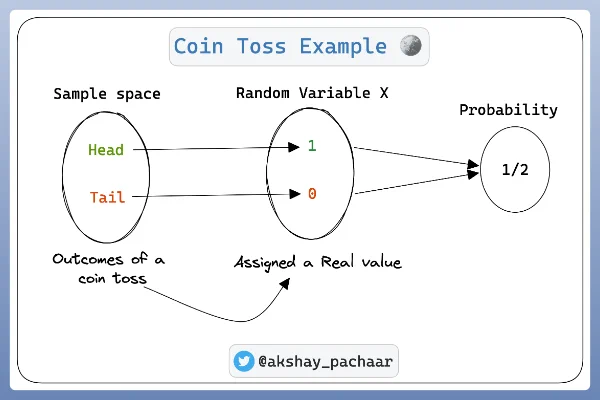
Probability distribution functions

• Two types of random variables

  • Discrete

  • Continuous

• The distribution of a random variable \(X\) describes the likelihood of the values that \(X\) can take

Discrete random variables: definition

• Discrete random variables are defined on a range that is a countable set

• i.e., they can only take on a finite or countably infinite number of different values

Probability mass function (PMF)

• Let \(X\) be a discrete random variable

• The probability mass function (PMF) of \(X\) summarizes the probability of each outcome \(x\)

• PMF: function \(p\) given by \[P(X = x)\]

  • \(X\) = RV

  • \(x\) = Outcome

Example: Dessert tonight

Imagine that you started a strict diet a few days ago. You are at a dinner party at your friend’s who made your favorite dessert. You are very tempted and make the decision to flip a coin three times. The number of times that the flip coin returns tail determines the number of bites of the dessert you will have. Before you start flipping the coin, you want to learn more about your chances of not having dessert tonight. To do that, you decide to look at the possible outcomes. You let 𝑋 be the number of times a series of three coin flips returns tails (T). The support of 𝑋 is {0, 1, 2, 3}.

Dessert tonight

PMF: Dessert tonight

Cumulative distribution function (CDF): definition

• The CDF of a random variable is the function \(F\) such that

  • \(F(x) = P(X \leq x)\)

• PMF tells us probability of each possible outcome

• CDF tells us the probability that an outcome below a specific value occurs

• Sums to 1

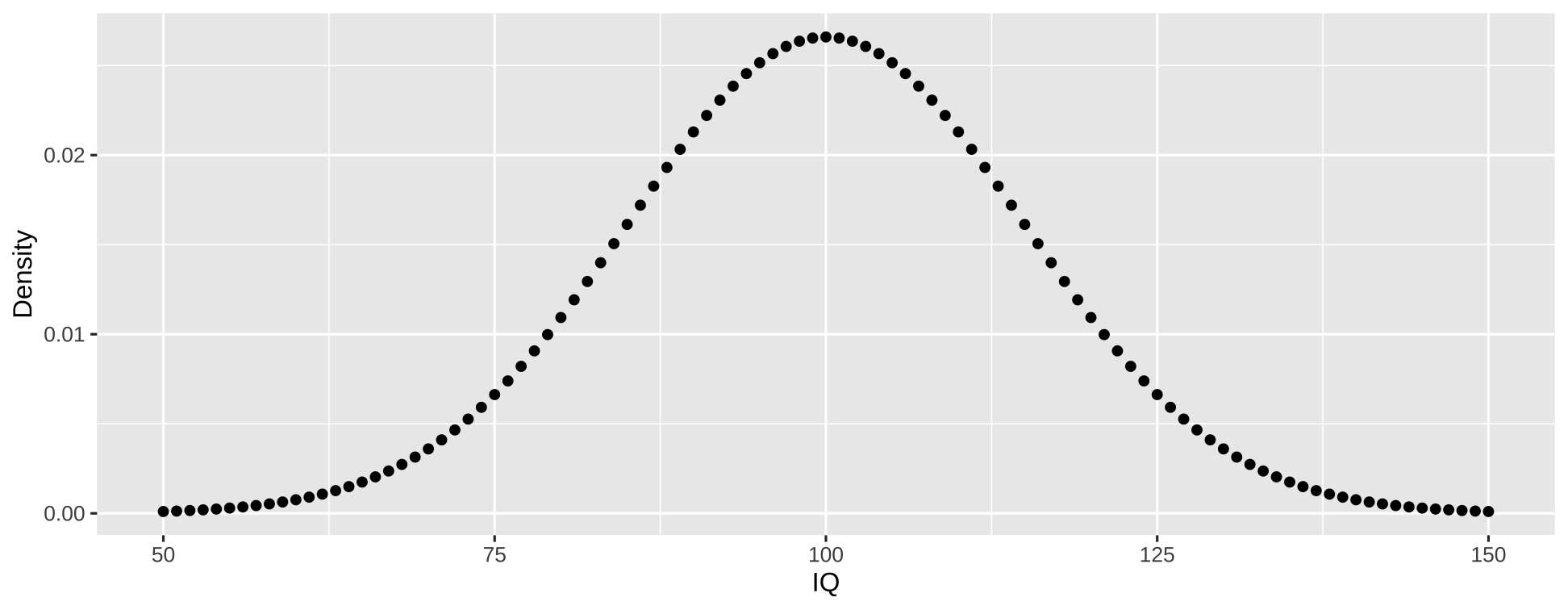
Continuous random variables: Definition

• A continuous random variable is a variable that can take on an infinite number of values within a given range or interval

Probability Density Function (PDF): Definition

• PDF is continuous version of PMF
• The PDF of a random continuous variable is the function \(F\) such that

\[P(a \leq X \leq b) = \int_{a}^{b} f(x) \, dx\]

• PDF tells us the probability of range of outcomes

• What is probability of observing IQ between 100 and 125?

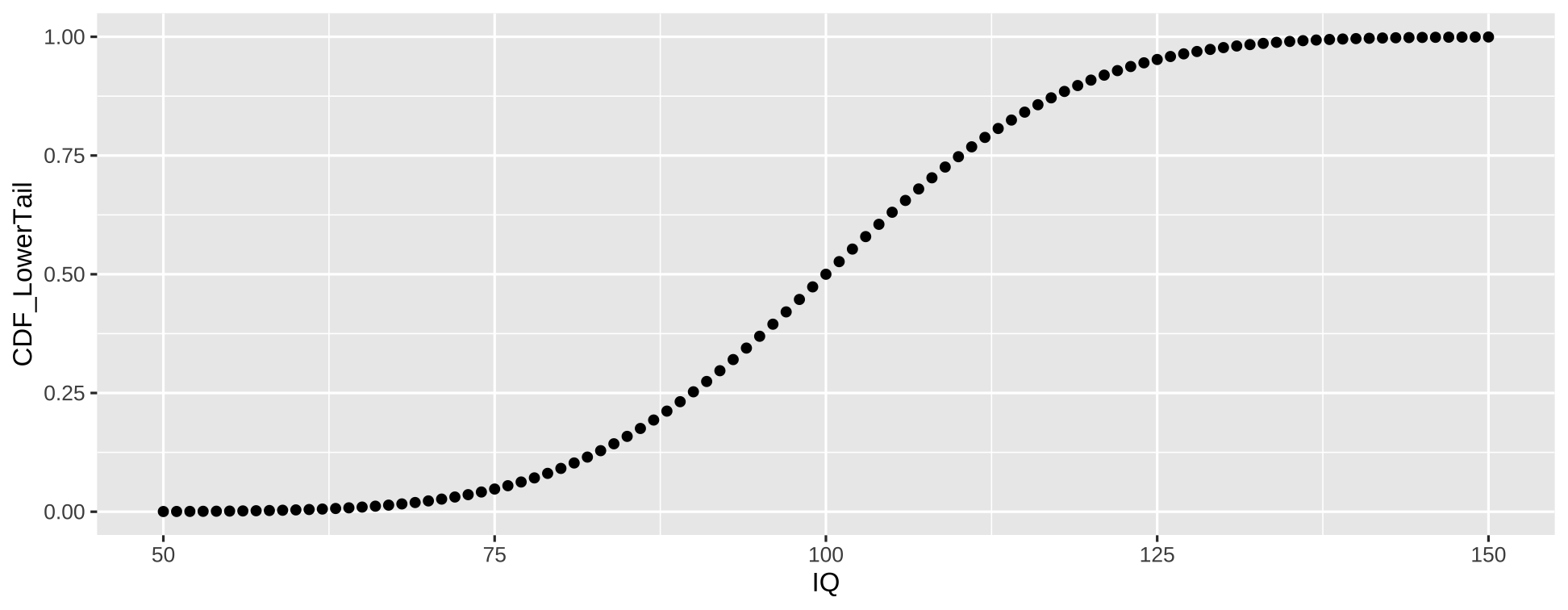
CDF

• \(F(x) = P(X \leq x)\)

  • \(IQ \leq 100\)

Summarizing random variables

• PMFs, PDFs, CDFs are very useful tools to summarize information from rvs.

• Many other ways to summarize random variables!

  • e.g., mean, median, standard deviation, etc.

Our goal as statisticians

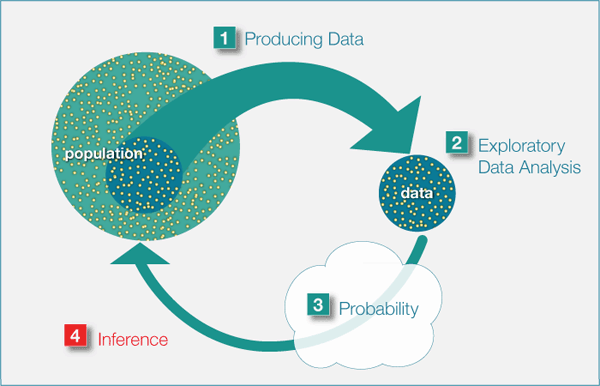
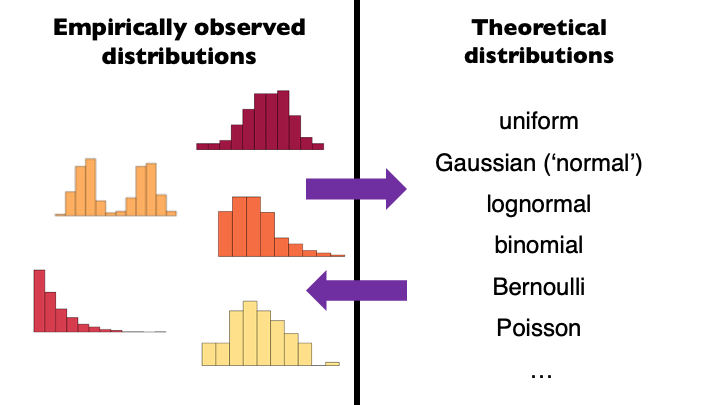
Link probability distributions to the data generating process (DGP)

• The DGP represents the “real-world” process of how data comes about

• Probability distributions are mathematical models used to model and understand the DGP

DGP

• Bottom-up: This approach begins with the observed data. By examining the data distribution, one might make educated guesses or inferences about the underlying processes that produced it

• Top-down: This approach relies on pre-existing knowledge or theories about the system or phenomenon in question to inform our understanding of the DGP

Bootstrapping

• • Sampling with replacement

    • A computer based method for deriving the probability distribution for any random variable

    • How to do it

      • Run your analysis a bunch of times with a slightly different set of observations each time

  • Dice roll

Once we have an idea about the DGP we can simulate data to see if it conforms to expectations.

Sampling helps us build up our intuitions about probability distributions

The book talks about dice rolls.

What are some others?

Bootstrapping

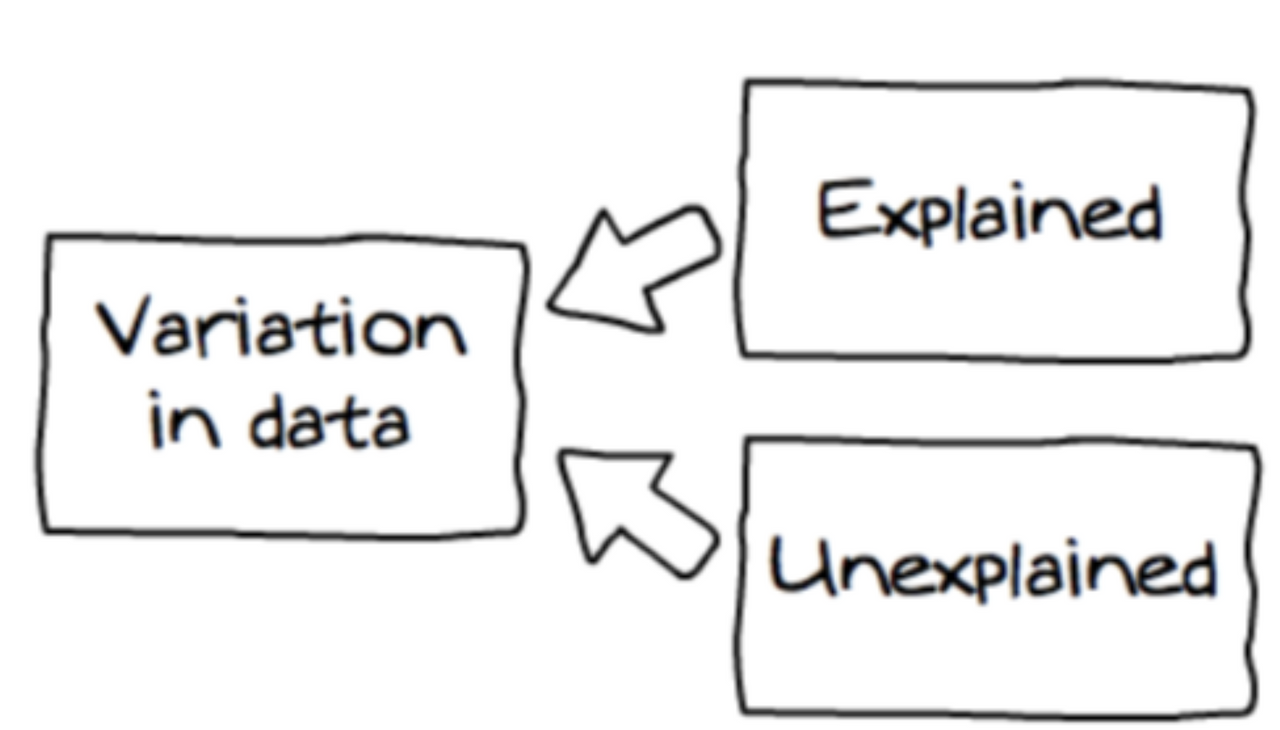
Sources of Variance

• There is uncertainty associated with the DGP

Types of Error

Unexplained Error

Sources of Unexplained Error

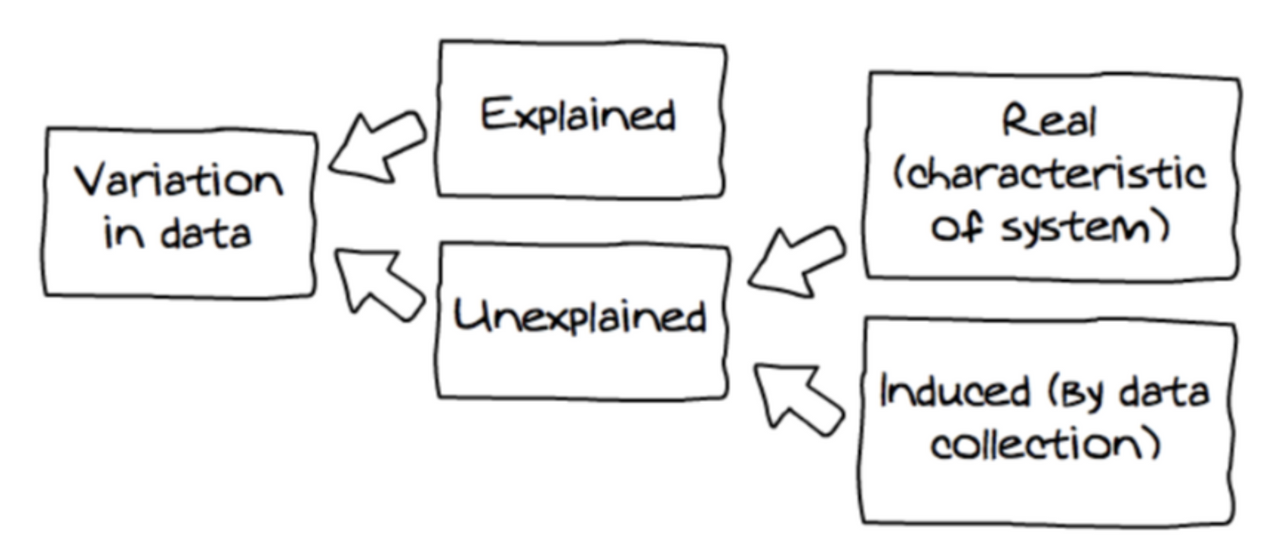
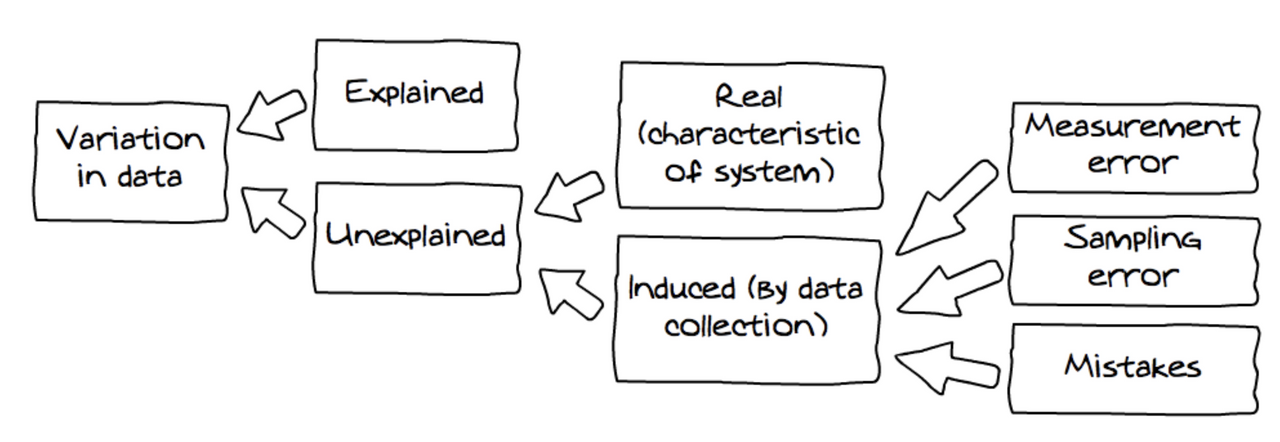
Randomness

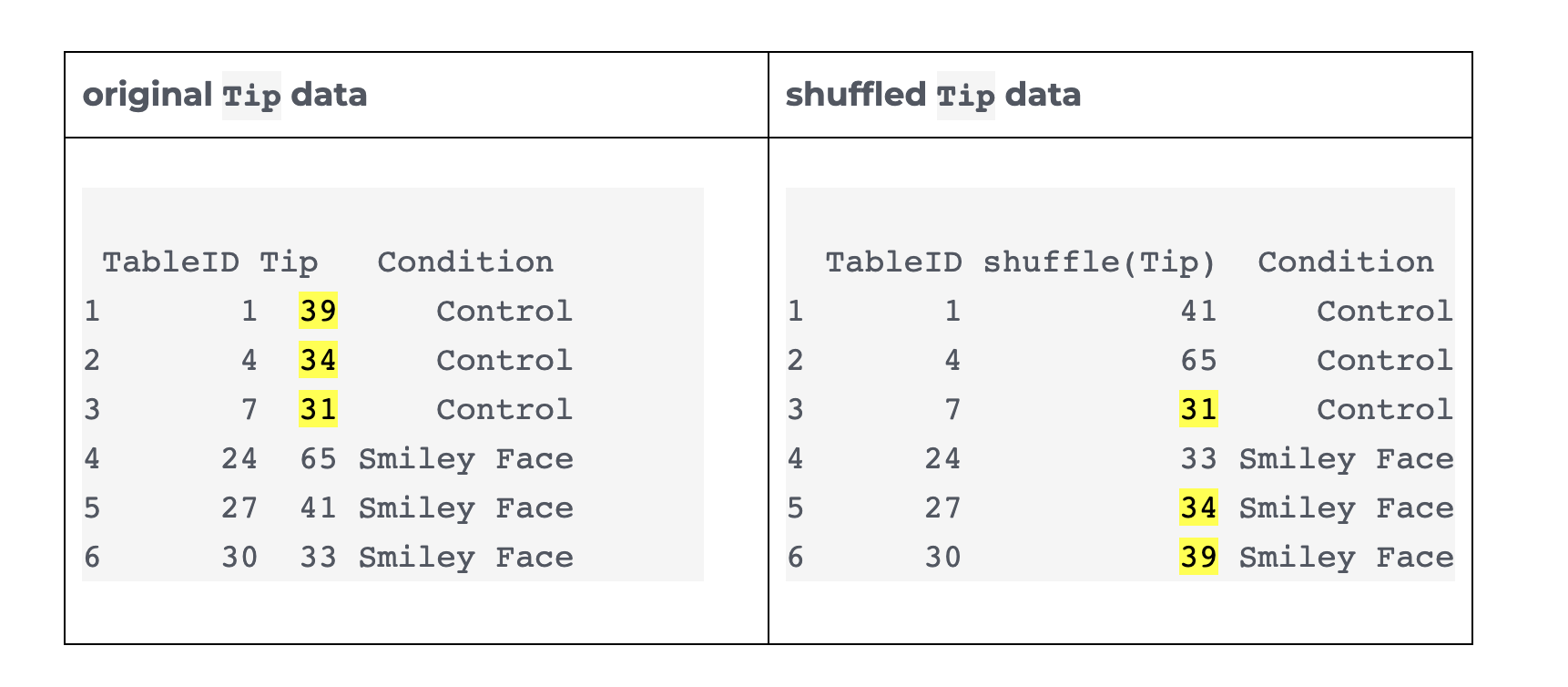
• Shuffling (permutation tests)

  @rind1996

  

Visualizing variance

• ggplot2 is tidyverse’s data visualization package (plotnine in Python uses similar syntax)

• The gg in ggplot2 stands for Grammar of Graphics

  • It is inspired by the book Grammar of Graphics by Leland Wilkinson

  • A grammar of graphics is a tool that enables us to concisely describe the components of a graphic

ggplot2

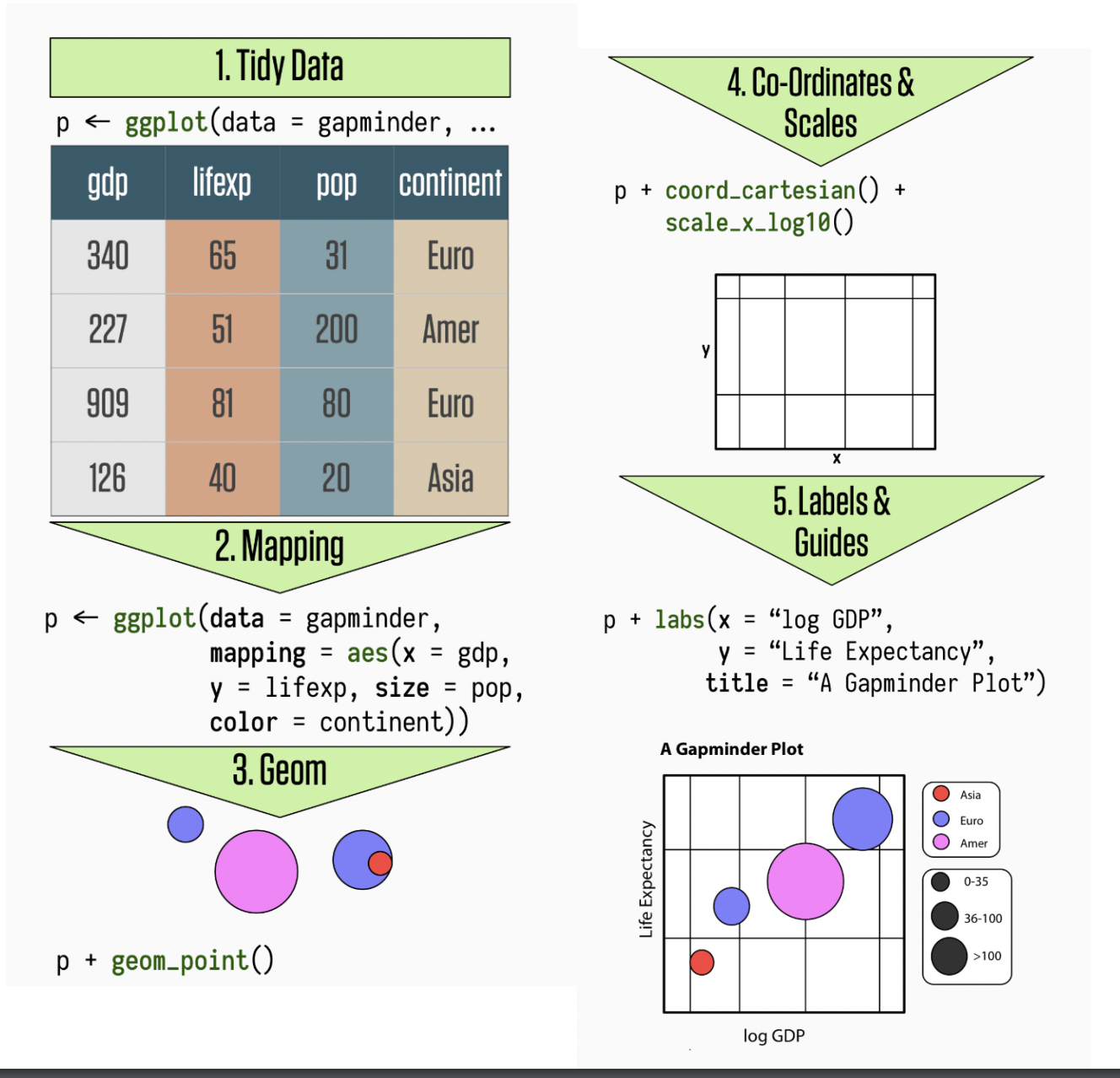
ggplot2

Let’s start with a blank canvas

ggplot2 - Data

ggplot2 - Layers

• Let’s add a geom

  • geom_point adds a dot for each raw data point

ggplot2 - Layers

• Let’s add another geom

  • geom_smooth plots a smoothed line for the data

ggplot2 Layers

• Maybe a linear line

ggplot2 - Layers

• It might be nice to see the raw data WITH the line. We can combine geoms!

ggplot2 - Size

• Points are a bit small. Let’s make them bigger!

ggplot2 - Color

• How could we add information about different types of penguins?

ggplot2- Axes

• Let’s clean up our plot

  • Add clearer axis labels

ggplot2 - Title

• Let’s clean up our plot

• Add title

ggplot2 - Themes

ggplot2 - Color themes

ggplot2 - Themes

Visualizing Variance and Relationships

Disclaimer

- More information is always better!

• Avoid visualizing single numbers when you have a whole distribution of numbers

Histograms

Histograms

• Put data into equally spaced buckets (or bins), plot how many rows are in each bucket

---

ggdist

• Put data into equally spaced buckets (or bins), plot how many rows are in each bucket

---

Histograms: Bin width

• Range of values in each bar or dot

  Narrow

  Big

  Perfect

---

Histogram tips

• Add a border to the bars
  for readability

  • geom_histogram(..., color = "green")

Histogram tips

• Set the boundary

Density plots

• Use calculus to find the probability of each x value

Density plots: Kernels and bandwidths

• Different options for calculus change the plot shape

  • Kernels - Smooth data points

  • bandwidth - how wide

Box plots

Box plots

• Show specific distributional numbers

Five number summary

Categorical Variables

Bar plots

Bar plots

Exploring quantitative variables

• Scatter plots

  

Categorical x Continuous

Exploring multiple groups

• Visualize the distribution of a
  single variable across groups

• Add a fill aesthetic or use faceting!

Multiple histograms

• This looks bad and is hard to read

Multiple histograms

Pyramid histograms

Multiple densities: Transparency

Multiple densities: Ridge plots

Multiple box plots

• Boxplots

Violin plots

• Density plot rotated 90 degrees and mirrored

Are violin plots bad?

Half violin plots + Box

Strip plots

Strip plots

• Add summary stats

Raincloud plots

Half violin plots + box + raw points

Raincloud Plots

Multiple Geoms

• Multiple Geoms

Categorical vs. Categorical

• Stacked bar plots

Combining plots

patchwork

cowplot

Cited